Holomorph of a group
A concept in group theory which arose in connection with the following problem. Is it possible to include any given group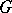 
as a normal subgroup in some other group so that all the automorphisms of 
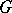are restrictions of inner automorphisms of this large group? To solve a problem of this kind, a new group 
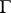is constructed using 
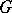and its automorphism group 
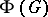. The elements of 
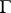are pairs 
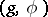where 
, 
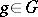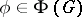, and composition of pairs is defined by the formula
 |
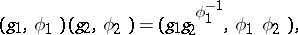where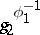 
is the image of 
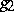under 
. The group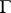 
(or a group isomorphic to it) is called the holomorph of 
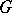. The set of pairs of the form 
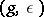, where 
is the identity element of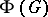 
, constitutes a subgroup that is isomorphic to the original group 
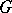. In a similar manner, the pairs of the form 
, where 
is the identity element of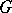 
, constitute a subgroup isomorphic to the group 
. The formula
 |
shows that 
is in fact a solution of the problem posed above.
Comments
References
| [a1] | M. Hall jr., "The theory of groups" , Macmillan (1959) |
| [a2] | A.G. Kurosh, "Theory of groups" , 1 , Chelsea (1955) (Translated from Russian) |
Holomorph of a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holomorph_of_a_group&oldid=47243