Hodograph transform

A mapping realizing a transformation of certain differential equations of mathematical physics to their linear form.

The Bernoulli integral and the continuity equation of a plane-parallel potential stationary motion of a barotropic gas ,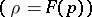

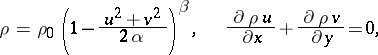where

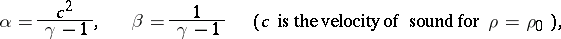lead to the equation

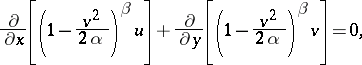which is used for determining the velocity potential

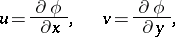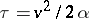where and are the velocity components. By introducing new independent variables and 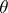equal to the slope of the angle made by the velocity vector with the -axis, equation

is reduced to linear form:

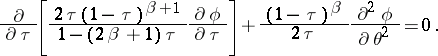This is the first hodograph transformation, or the Chaplygin transformation. The second Chaplygin transformation is obtained by applying the tangential Legendre transform. The function

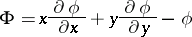is selected as the new unknown; it is expressed in terms of new independent variables and , which replace and by the formulas

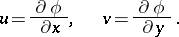The equation

assumes a linear form:

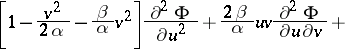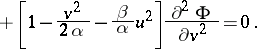Hodograph transforms are employed in solving problems in the theory of flow and of streams of gases flowing around curvilinear contours.

References

[1]	S.A. Chaplygin, "On gas-like structures" , Moscow-Leningrad (1949) (In Russian)
[2]	N.E. Kochin, I.A. Kibel', N.V. Roze, "Theoretical hydrodynamics" , Interscience (1964) (Translated from Russian)

References

[a1]	N. Curle, H.J. Davies, "Modern fluid dynamics" , 1–2 , v. Nostrand-Reinhold (1971)