Hilbert singular integral

The improper integral (in the sense of the Cauchy principal value)

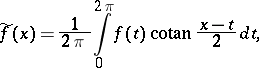where the periodic function 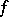is called the density of the Hilbert singular integral, while 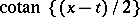is called its kernel. If 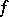is summable, 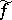exists almost-everywhere; if 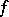satisfies the Lipschitz condition of order 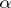, , 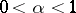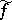exists for any and satisfies this condition as well. If 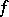has summable 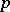-th power, 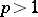, 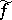has the same property, and

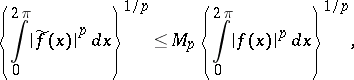where 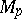is a constant independent of 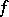. In addition, the inversion formula of Hilbert's singular integral,

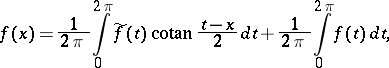is valid. The function 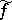is said to be conjugate with .

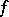References

[1]	D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953)
[2]	M. Riesz, "Sur les fonctions conjugées" Math. Z. , 27 (1927) pp. 218–244
[3]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)
[4]	N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian)

Comments

See also Hilbert kernel; Hilbert transform.

References

[a1]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988)
[a2]	B.L. Moiseiwitsch, "Integral equations" , Longman (1977)