Hermitian connection
An affine connection on a Hermitian manifold 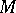 relative to which the tensor
relative to which the tensor  defined by the complex structure and the fundamental
defined by the complex structure and the fundamental  -form
-form 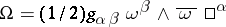 are parallel, implying the same property for the Hermitian form
are parallel, implying the same property for the Hermitian form  . If the affine connection on
. If the affine connection on 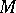 is given by local connection forms
is given by local connection forms 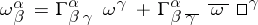 , then these conditions can be expressed as
, then these conditions can be expressed as
 |
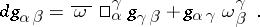 |
On a given Hermitian manifold 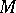 there is one and only one Hermitian connection for which
there is one and only one Hermitian connection for which 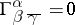 .
.
A generalization is an almost-Hermitian connection, which is defined by similar conditions on the tensors 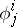 and
and  with
with 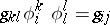 on an almost-Hermitian manifold
on an almost-Hermitian manifold 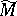 . An almost-Hermitian connection on a given
. An almost-Hermitian connection on a given 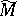 exists. It is uniquely defined by its torsion tensor: If the torsion tensors of two almost-Hermitian connections are the same, then so are the connections. For example, there is one and only one almost-Hermitian connection for which the torsion forms are sums of "pure" forms (that is, forms of type
exists. It is uniquely defined by its torsion tensor: If the torsion tensors of two almost-Hermitian connections are the same, then so are the connections. For example, there is one and only one almost-Hermitian connection for which the torsion forms are sums of "pure" forms (that is, forms of type 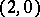 and
and 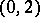 ), namely, the second canonical Lichnerowicz connection.
), namely, the second canonical Lichnerowicz connection.
References
| [1] | A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French) |
| [2] | K. Yano, "Differential geometry on complex and almost complex spaces" , Pergamon (1965) |
Comments
The first and second canonical connections on an almost-Hermitian manifold are described in [1], p. 192 and pp. 194-195, respectively.
References
| [a1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969) |
| [a2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
Hermitian connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermitian_connection&oldid=47218