Hermite transform
From Encyclopedia of Mathematics
The integral
 |
where 
are the Hermite polynomials. The inversion formula is
 |
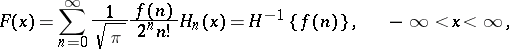provided that the series converges. The Hermite transform reduces the operator
 |
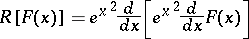to an algebraic one by the formula
 |
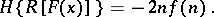If 
and all its derivatives up to and including the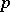 
-th order are bounded, then
 |
The Hermite transform has also been introduced for a special class of generalized functions (see [2]). They are used to solve differential equations containing the operator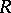 
.
References
| [1] | L. Debnath, "On the Hermite transform" Mat. Vesnik , 1 (1964) pp. 285–292 |
| [2] | A.G. Zemanian, "Generalized integral transforms" , Wiley (1968) |
How to Cite This Entry:
Hermite transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermite_transform&oldid=47217
Hermite transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermite_transform&oldid=47217
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article