Hermite interpolation formula
A form of writing the polynomial  of degree
of degree 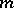 that solves the problem of interpolating a function
that solves the problem of interpolating a function  and its derivatives at points
and its derivatives at points  , that is, satisfying the conditions
, that is, satisfying the conditions
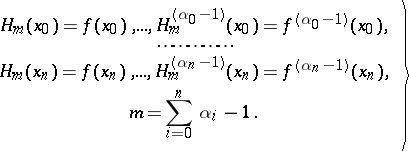 | (1) |
The Hermite interpolation formula can be written in the form
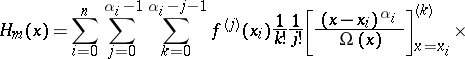 |
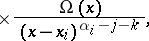 |
where  .
.
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
Comments
Hermite interpolation can be regarded as a special case of Birkhoff interpolation (also called lacunary interpolation). In the latter, not all values of a function  and its derivatives are known at given points
and its derivatives are known at given points 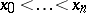 (whereas there is complete information in the case of Hermite interpolation). Data such as (1) naturally give rise to a matrix
(whereas there is complete information in the case of Hermite interpolation). Data such as (1) naturally give rise to a matrix 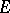 , a so-called interpolation matrix, constructed as follows. Write
, a so-called interpolation matrix, constructed as follows. Write  for
for 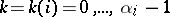 and
and 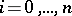 . Put
. Put 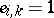 if the constant
if the constant  is known (given) and
is known (given) and  if it is not (for Hermite interpolation all
if it is not (for Hermite interpolation all 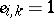 ). Now
). Now  .
.
Such a matrix 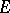 is called order regular if it is associated to a solvable problem (i.e. (1) is solvable for all choices of
is called order regular if it is associated to a solvable problem (i.e. (1) is solvable for all choices of 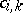 for which
for which 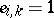 ). (Similarly, if the set
). (Similarly, if the set  of interpolation points may vary over a given class, a pair
of interpolation points may vary over a given class, a pair  is called regular if (1) is solvable for all
is called regular if (1) is solvable for all 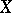 in this class and all choices of
in this class and all choices of 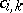 for which
for which 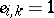 .) A basic theme in Birkhoff interpolation is to find the regular pairs
.) A basic theme in Birkhoff interpolation is to find the regular pairs 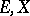 . More information can be found in [a1].
. More information can be found in [a1].
References
| [a1] | G.G. Lorentz, K. Jetter, S.D. Riemenschneider, "Birkhoff interpolation" , Addison-Wesley (1983) |
| [a2] | I.P. Mysovskih, "Lectures on numerical methods" , Wolters-Noordhoff (1969) pp. Chapt. 2, Sect. 10 |
| [a3] | B. Wendroff, "Theoretical numerical analysis" , Acad. Press (1966) pp. Chapt. 1 |
Hermite interpolation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermite_interpolation_formula&oldid=47214