Hausdorff summation method
A summation method for series of numbers or functions, introduced by F. Hausdorff [1]; it is defined as follows. A sequence  is subjected in succession to three linear matrix transformations:
is subjected in succession to three linear matrix transformations:
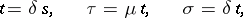 |
where  is the transformation by means of the triangular matrix
is the transformation by means of the triangular matrix  :
:
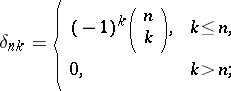 |
and  is the diagonal transformation by means the diagonal matrix
is the diagonal transformation by means the diagonal matrix  :
:
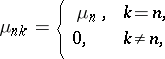 |
where  is a numerical sequence. The transformation
is a numerical sequence. The transformation
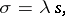 |
where 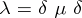 ,
, 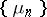 is an arbitrary numerical sequence, is called a general Hausdorff transformation, and the matrix
is an arbitrary numerical sequence, is called a general Hausdorff transformation, and the matrix 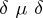 — a Hausdorff matrix. Written out, a general Hausdorff transformation has the form
— a Hausdorff matrix. Written out, a general Hausdorff transformation has the form
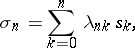 |
where
 |
 |
The series
 |
with partial sums  is summable by the Hausdorff method to sum
is summable by the Hausdorff method to sum  if
if
 |
The field and the regularity of the Hausdorff method depend on the sequence  . If
. If 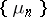 is a real sequence, then for the regularity of the method it is necessary and sufficient that
is a real sequence, then for the regularity of the method it is necessary and sufficient that 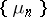 is the difference of two absolutely-monotone sequences and that
is the difference of two absolutely-monotone sequences and that
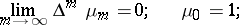 |
or, in another terminology, necessary and sufficient is that the 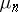 are regular moments.
are regular moments.
The Hausdorff summation method contains as special cases a number of other well-known summation methods. Thus, for  the Hausdorff method turns into the Euler method
the Hausdorff method turns into the Euler method  , for
, for 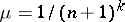 into the Hölder method
into the Hölder method 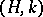 , and for
, and for
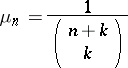 |
into the Cesàro method 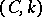 .
.
References
| [1] | F. Hausdorff, "Summationsmethoden und Momentfolgen I, II" Math. Z. , 9 (1921) pp. 74–109; 280–299 |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Hausdorff summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hausdorff_summation_method&oldid=47199