Harmonizable random process
A complex-valued random function 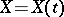 of a real parameter
of a real parameter  which may be represented as a stochastic integral:
which may be represented as a stochastic integral:
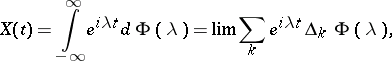 | (*) |
where 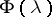 ,
, 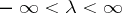 , is a random process. The increments
, is a random process. The increments 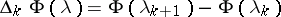 in (*) define random "amplitudes"
in (*) define random "amplitudes" 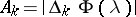 and "phases"
and "phases" 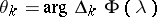 of elementary vibrations of the form
of elementary vibrations of the form
 |
of frequencies 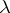 ,
, 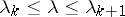 , the superposition of which yields, in the limit,
, the superposition of which yields, in the limit,  . The (mean-square) limit in the representation (*) is taken along a sequence of successively-finer subdivisions of the line
. The (mean-square) limit in the representation (*) is taken along a sequence of successively-finer subdivisions of the line 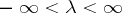 into intervals
into intervals 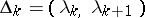 with
with 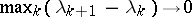 . It is usually assumed that
. It is usually assumed that
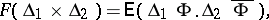 |
as a function of the sets  in the plane, defines a complex measure of bounded variation; in this case the corresponding process
in the plane, defines a complex measure of bounded variation; in this case the corresponding process 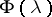 ,
,  (or, more exactly, the corresponding random measure
(or, more exactly, the corresponding random measure 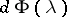 ), is unambiguously defined by the process
), is unambiguously defined by the process 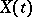 ,
, 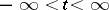 , itself:
, itself:
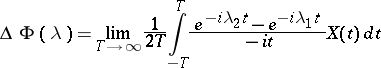 |
for any interval 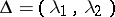 such that
such that 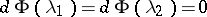 , and
, and
 |
for any point 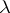 ,
, 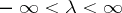 . A random process
. A random process 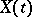 ,
, 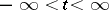 , is harmonizable if and only if its covariance is representable in the form
, is harmonizable if and only if its covariance is representable in the form
 |
Examples of harmonizable random processes.
1) A modulated stationary random process. If
 |
is a stationary random process, a process of the form
 |
where  , where
, where 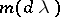 is a measure on the line, is usually no longer stationary, but will be harmonizable:
is a measure on the line, is usually no longer stationary, but will be harmonizable:
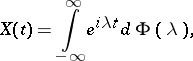 |
where the random measure 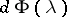 is defined by the formula
is defined by the formula
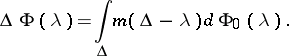 |
2) A process defined by sliding summation (or moving averages)
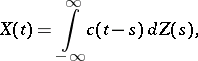 |
where 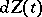 is some random measure on the line and the weight function
is some random measure on the line and the weight function  is of the same type as above:
is of the same type as above:
 |
In this case
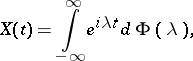 |
where
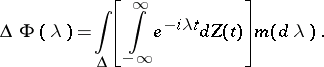 |
References
| [1] | M. Loève, "Probability theory" , 2 , Springer (1978) |
Harmonizable random process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harmonizable_random_process&oldid=47186