Harmonic measure, principle of

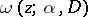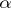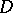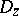The harmonic measure does not decrease under mappings realized by single-valued analytic functions. If is the harmonic measure of a boundary set with respect to a domain in the complex -plane, one specific formulation of the principle of harmonic measure is as follows. In a domain with boundary 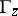consisting of a finite number of Jordan arcs let there be given a single-valued analytic function 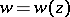which satisfies the following conditions: the values 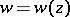, , 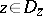form part of the domain 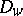with boundary 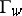consisting of a finite number of Jordan arcs; the function 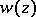can be continuously extended onto some set 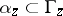consisting of a finite number of arcs; and the values of 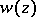on 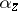form part of a set 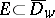with boundary 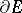consisting of a finite number of Jordan arcs. Under these conditions one has, at any point 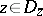at which ,

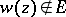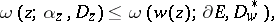(1)

where 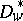denotes the subdomain of 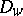such that 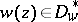and 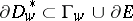. If (1) becomes an equality at any point , then equality will be valid everywhere in 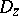. In particular, for a one-to-one conformal mapping from 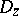onto 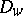one has the identity

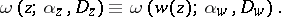The principle of harmonic measure, including its numerous applications [1], [2], was established by R. Nevanlinna. In particular, a corollary of the principle is the two-constants theorem, which implies, in turn, that for a function 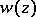that is holomorphic in a domain 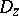, the maximum value of 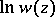on the level line 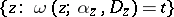is a convex function of the parameter .

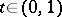The principle of harmonic measure has been generalized to holomorphic functions 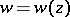, , 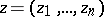of several complex variables, .

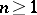References

[1]	F. Nevanlinna, R. Nevanlinna, "Ueber die Eigenschaften einer analytischen Funktion in der Umgebung einer singulären Stelle oder Linie" Acta Soc. Sci. Fennica , 50 : 5 (1922) pp. 1–46
[2]	R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German)