Hardy inequality
From Encyclopedia of Mathematics
for series
If  ,
,  and
and  ,
,  then
then
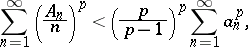 |
except when all the  are zero. The constant
are zero. The constant  in this inequality is best possible.
in this inequality is best possible.
The Hardy inequalities for integrals are:
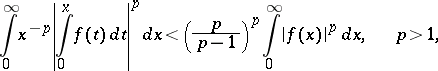 |
and
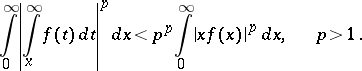 |
The inequalities are valid for all functions for which the right-hand sides are finite, except when  vanishes almost-everywhere on
vanishes almost-everywhere on  . (In this case the inequalities turn into equalities.) The constants
. (In this case the inequalities turn into equalities.) The constants 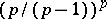 and
and  are best possible.
are best possible.
The integral Hardy inequalities can be generalized to arbitrary intervals:
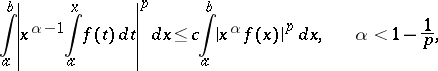 |
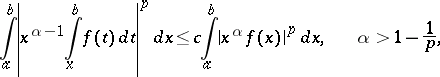 |
where  ,
,  , and where the
, and where the  's are certain constants.
's are certain constants.
Generalized Hardy inequalities are inequalities of the form
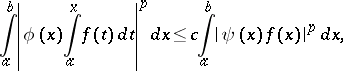 | (1) |
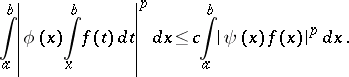 | (2) |
If 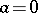 and
and  , inequality (1) holds if and only if
, inequality (1) holds if and only if
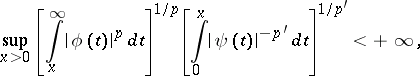 |
and (2) holds if and only if
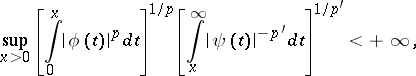 |
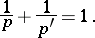 |
References
| [1] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) |
| [2] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [3] | B. Muckenhoupt, "Hardy's inequality with weights" Studia Math. , 44 (1972) pp. 31–38 |
How to Cite This Entry:
Hardy inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_inequality&oldid=47176
Hardy inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_inequality&oldid=47176
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article