Hardy criterion

for uniform convergence of series of functions

If a sequence of real-valued functions , 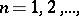is monotone for every 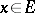, where 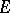is a certain set, and converges uniformly to zero on 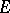, and if the sequence of partial sums of a series 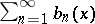is bounded on 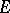(the functions may take complex values), then the series 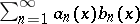converges uniformly on .

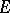This criterion was established by G.H. Hardy [1].

References

[1]	G.H. Hardy, "Some theorems connected with Abel's theorem on the continuity of power series" Proc. London. Math. Soc. (2) , 4 (1907) pp. 247–265

Comments

This criterion can be proved using the Euler–MacLaurin formula (cf. the proof of Thm. 3.42 in [a1]).

References

[a1]	W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 107–108