Halász mean value theorem

Considerable interest has been devoted to the problem of obtaining conditions for arithmetic functions (cf. Arithmetic function), in particular for multiplicative functions (cf. Multiplicative arithmetic function), that guarantee the existence of a mean value

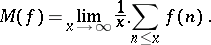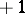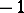A strong motivation for this interest was the famous Erdös–Wintner conjecture (see [a2]): Any multiplicative function assuming only the values and possesses a mean value.

Around 1961, theorems of H. Delange (see Delange theorem) and E. Wirsing (see Wirsing theorems) gave a satisfactory answer for multiplicative functions with non-zero mean value. However, a general mean value theorem, containing a proof of the prime number theorem (cf. also de la Vallée-Poussin theorem) and of the Erdös–Wintner conjecture, was only given by Wirsing in 1967 (see [a7]) and G. Halász in 1968 (see [a3]).

A simple form of Halász' theorem reads as follows: If 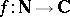is a multiplicative function, 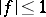, then there exist constants 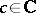, , 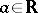and a slowly oscillating function 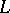, satisfying , such that

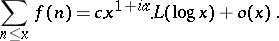In particular, if 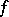is real-valued, then 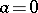, , 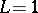and so 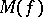exists. For the proof, Halász used the classical method of complex integration (cf. Contour integration, method of) in a very skilful way.

A more precise formulation (see [a3], Satz 2) is as follows. Assume that 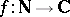is multiplicative and that .

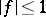i) If the series 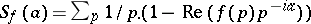diverges for all 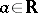, then 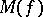exists and is equal to zero.

ii) If for some 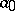the series 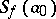is convergent, then, as ,

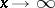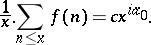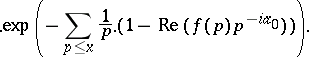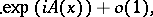where .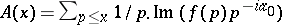

The unpleasant condition 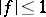in the theorem was (partly) removed, and remainder estimates were given, in, e.g., [a4], [a8], [a9]. K.-H. Indlekofer [a6] gave a version of the theorem for the class of "uniformly summable" multiplicative functions. A uniformly summable multiplicative function is a multiplicative function satisfying

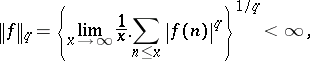and

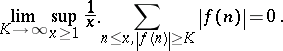In 1988, A. Mačiulis gave a version of Halász' theorem with remainder term. Elementary proofs of the Halász theorem were published in [a1].

References

[a1]	H. Daboussi, K.-H. Indlekofer, "Two elementary proofs of Halász's theorem" Math. Z. , 209 (1992) pp. 43–52
[a2]	P. Erdös, "Some unsolved problems" Michigan Math. J. , 4 (1957) pp. 291–300
[a3]	G. Halász, "Über die Mittelwerte multiplikativer zahlentheoretischer Funktionen" Acta Math. Acad. Sci. Hung. , 19 (1968) pp. 365–403
[a4]	G. Halász, "On the distribution of additive and the mean values of multiplicative arithmetic functions" Studia Sci. Math. Hung. , 6 (1971) pp. 211–233
[a5]	G. Halász, "Remarks to my paper "On the distribution of additive and the mean values of multiplicative arithmetic functions" " Acta Math. Acad. Sci. Hung. , 23 (1972) pp. 425–432
[a6]	K.-H. Indlekofer, "Remark on a theorem of G. Halász" Archiv Math. , 36 (1981) pp. 145–151
[a7]	E. Wirsing, "Das asymptotische Verhalten von Summen über multiplikative Funktionen, II" Acta Math. Acad. Sci. Hung. , 18 (1967) pp. 414–467
[a8]	A. Parson, J. Tull, "Asymptotic behavior of multiplicative functions" J. Number Th. , 10 (1978) pp. 395–420
[a9]	M.I. Tuljaganova, "A generalization of a theorem of Halász" Izv. Akad. Nauk UzSSR , 4 (1978) pp. 35–40; 95 (In Russian)