Growth indicatrix
indicator of an entire function
The quantity
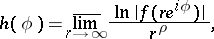 |
characterizing the growth of an entire function  of finite order
of finite order  and finite type
and finite type  along the ray
along the ray  for large
for large  (
( ). For instance, for the function
). For instance, for the function
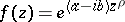 |
the order is 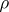 and the growth indicatrix is equal to
and the growth indicatrix is equal to 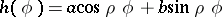 ; for the function
; for the function 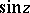 the order is
the order is 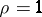 and
and 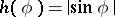 . The function
. The function 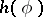 is everywhere finite, continuous, has at each point left and right derivatives, has a derivative everywhere except possibly at a countable number of points,
is everywhere finite, continuous, has at each point left and right derivatives, has a derivative everywhere except possibly at a countable number of points,  always and there is at least one
always and there is at least one 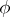 for which
for which 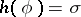 , has the characteristic property of trigonometric convexity, i.e. if
, has the characteristic property of trigonometric convexity, i.e. if
 |
 |
 |
then
 |
The following inequality holds:
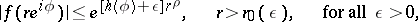 |
where 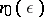 is independent of
is independent of 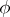 .
.
The growth indicatrix is also introduced for functions that are analytic in an angle and in this angle are of finite order or have a proximate order and are of finite type.
References
| [1] | B.Ya. Levin, "Distribution of zeros of entire functions" , Amer. Math. Soc. (1980) (Translated from Russian) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
Comments
Indicators of entire functions of several variables have been introduced also; e.g. Lelong's regularized radial indicator:
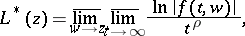 |
where  is an entire function of order
is an entire function of order 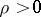 and of finite type on
and of finite type on  ,
, 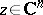 . (If
. (If 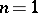 :
:  .)
.)
The indicator 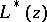 is a
is a 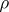 -homogeneous plurisubharmonic function. This corresponds with the convexity properties of the one-dimensional case. However, in general it is not a continuous function.
-homogeneous plurisubharmonic function. This corresponds with the convexity properties of the one-dimensional case. However, in general it is not a continuous function.
References
| [a1] | L.I. Ronkin, "Inroduction to the theory of entire functions of several variables" , Transl. Math. Monogr. , 44 , Amer. Math. Soc. (1974) (Translated from Russian) |
| [a2] | P. Lelong, L. Gruman, "Entire functions of several variables" , Springer (1986) |
| [a3] | R.P. Boas, "Entire functions" , Acad. Press (1954) |
Growth indicatrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Growth_indicatrix&oldid=47146