Geometro-dynamics

A variant of unified field theory which reduces all physical objects to geometric objects. Geometro-dynamics is constructed in several stages.

The first stage consists of the construction of a unified theory of gravitation and electromagnetism on the basis of general relativity theory. The principal problems of geometro-dynamics at this stage may be stated in a simplified manner as follows. Let there be given a metric 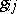of space-time which is a solution of Einstein's equations

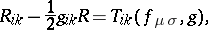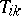where is the Ricci tensor, is the energy-momentum tensor of the electromagnetic field in vacuum, and is the field-strength tensor of the electromagnetic field that satisfies the Maxwell equations. The task is to express in terms of . When put in this simplified manner, the problem has a solution in principle [1], but its complete solution presents difficulties (such as allowance for non-electromagnetic fields) which have not yet (1988) been overcome.

The second stage consists of the construction of a theory of elementary particles. The model of a pair of interacting particles is the so-called "handle" , the simplest form of which is one of the topological interpretations [2] of the maximal analytic extension of the Schwarzschild field. In this model the characteristics (e.g. the charge) of an elementary particle are given by certain integer invariants of the "handle" . In geometro-dynamics space-time is multiply connected, while its first Betti number is of the same order as the number of particles. The concept of a geon was introduced — a wave packet of some given radiation of a concentration which is sufficient for the corresponding distortion of space to make this wave packet metastable (i.e. existing for a long time). Geometro-dynamics predicts electro-magnetic, neutrino and gravitational geons. The concept of a geon is classical. It is believed that the quantum analogue of the concept of geometro-dynamics is a geometro-dynamic description of the mass of elementary particles (geons have not been experimentally observed).

The third stage consists in the construction of a theory of continuous media which yields, broadly speaking, the same results as does the general theory of relativity.

It is assumed that geometro-dynamics involves a violation of the law of conservation of baryon charge. A concrete example of this is the process of gravitational collapse and subsequent evaporation of black holes.

The fourth stage consists of attempts to subsequently construct a quantum geometro-dynamics. Quantum fluctuations of the metric are considered, and it is proved that at a distance of order 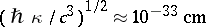(where is the Planck constant, 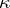is Einstein's gravitational constant and is the velocity of light) such fluctuations can substantially alter the topology of space-time and must correspond to elementary quantum particles.

At the time of writing (1970s) geometro-dynamics is not yet a fully developed theory. The interpretation of spin fields (as distinct from tensor fields), in particular of neutrino fields, is especially difficult. Many features of geometro-dynamics have no adequate mathematical foundation. The theory of superspace [4] is one attempt to provide such a foundation.

References

[1]	G.Y. Rainich, "Electrodynamics in general relativity theory" Trans. Amer. Math. Soc. , 27 (1925) pp. 106–136
[2]	J.A. Wheeler, "Geometrodynamics" , Acad. Press (1962)
[3]	B.K. Harrison, K.S. Thorne, M. Wakano, J.A. Wheeler, "Gravitational theory and gravitational collapse" , Univ. Chicago Press (1965)
[4]	Ya.B. Zel'dovich, I.D. Novikov, "Relativistic astrophysics" , 2. Structure and evolution of the universe , Chicago (1983) (Translated from Russian)

References

[a1]	J.A. Wheeler, "Some implications of general relativity for the structure and evolution of the universe" , XI Conseil de Physique Solvay. Bruxelles (1958) pp. 97–148