Gell-Mann formula
A prescription for constructing anti-Hermitian representations of a symmetric Lie algebra (over the real numbers)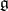 
from representations of an Inönü–Wigner contraction 
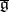. One assumes that 
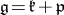is a direct sum of vector spaces and
 |
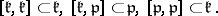Then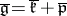 
and there exists an isomorphism of vector spaces 
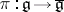such that 
, 
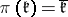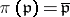and 
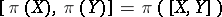for all 
, 
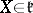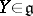. In addition, one has 
.
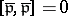The best studied examples concern the (pseudo-) orthogonal algebras, when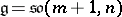 
or 
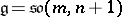and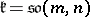 
[a1], [a2]. Then 
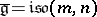is an inhomogeneous Lie algebra with 
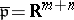. Let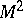 
be the quadratic 
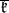-invariant element from the symmetric algebra of 
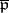. If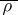 
is an anti-Hermitian representation of 
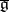such that 
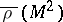is a multiple of the unit operator, then the formula for the representation 
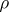of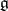 
reads: 
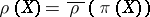for all 
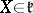, and, for all 
,
 |
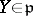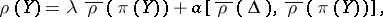where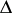 
is the second-degree Casimir element from the universal enveloping algebra of 
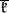while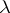 
and 
are parameters. Here, 
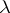is real and arbitrary and 
is pure imaginary and depends on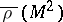 
.
References
| [a1] | E. Weimar, "The range of validity of the Gell-Mann formula" Nuovo Cim. Lett. , 4 (1972) pp. 43–50 |
| [a2] | R. Hermann, "Lie groups for physicists" , Benjamin (1966) |
Gell-Mann formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gell-Mann_formula&oldid=47062