Gegenbauer transform
The integral transform  of a function
of a function  ,
,
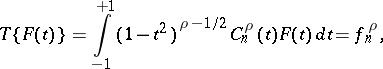 |
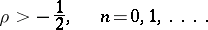 |
Here  are the Gegenbauer polynomials. If a function can be expanded into a generalized Fourier series by Gegenbauer polynomials, the following inversion formula is valid:
are the Gegenbauer polynomials. If a function can be expanded into a generalized Fourier series by Gegenbauer polynomials, the following inversion formula is valid:
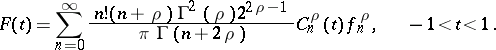 |
The Gegenbauer transform reduces the differentiation operation
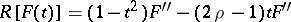 |
to the algebraic operation
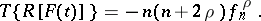 |
References
| [1] | V.A. Ditkin, A.P. Prudnikov, "Operational calculus" Progress in Math. , 1 (1968) pp. 1–75 Itogi Nauk. Ser. Mat. Anal. 1966 (1967) pp. 7–82 |
Comments
For any system of orthogonal polynomials one can formally consider a transform pair as above, cf.
and
in Fourier series in orthogonal polynomials. The Gegenbauer transform (and, more generally, the Jacobi transform) has been considered for arguments  which are arbitrarily complex. Then inversion formulas exist in the form of integrals and there is a relationship with sampling theory, cf. [a1], [a2].
which are arbitrarily complex. Then inversion formulas exist in the form of integrals and there is a relationship with sampling theory, cf. [a1], [a2].
References
| [a1] | P.L. Butzer, R.L. Stens, M. Wehrens, "The continuous Legendre transform, its inverse transform, and applications," Internat. J. Math. Sci. , 3 (1980) pp. 47–67 |
| [a2] | T.H. Koornwinder, G.G. Walter, "The finite continuous Jacobi transform and its inverse" J. Approx. Theory (To appear) |
Gegenbauer transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gegenbauer_transform&oldid=47057