Gauss transform

The linear functional transform 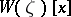of a function defined by the integral

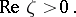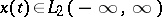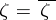If , then ; for real values , the operator 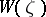is self-adjoint [1]. The inversion formula for the Gauss transform is

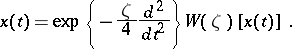If 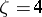, the Gauss transform is known as the Weierstrass transform.

References

[1]	E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957)
[2]	V.A. Ditkin, A.P. Prudnikov, "Integral transforms" Itogi Nauk. Ser. Mat. Mat. Anal. (1966) pp. 7–82 (In Russian)

Comments

The above inversion formula can be interpreted in terms of semi-groups. Another way to invert the Gauss transform is to write in the first equation 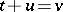, from which substitution a double-sided Laplace transform results. Then the inversion formula follows from well-known Laplace-transform techniques.

References

[a1]	I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972)