Gauss method
A method of successive elimination of unknowns in solving a set of linear equations, first introduced by C.F. Gauss [1]. Let there be given a system
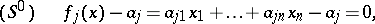 |
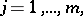 |
where 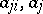 are elements of an arbitrary field
are elements of an arbitrary field 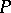 . Without loss of generality one may assume that
. Without loss of generality one may assume that 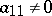 . The Gauss method operates as follows. One subtracts the first equation of the set, multiplied by
. The Gauss method operates as follows. One subtracts the first equation of the set, multiplied by 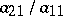 term by term, from the second equation; then one subtracts the first equation multiplied by
term by term, from the second equation; then one subtracts the first equation multiplied by 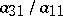 from the third equation;
from the third equation; 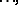 then one subtracts the first equation multiplied by
then one subtracts the first equation multiplied by 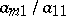 from the
from the 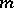 -th equation. Let
-th equation. Let 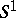 be the system of subtracted equations thus obtained. If a coefficient in
be the system of subtracted equations thus obtained. If a coefficient in 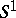 is non-zero (possibly after changing the sequence of equations and unknowns),
is non-zero (possibly after changing the sequence of equations and unknowns), 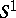 is treated as
is treated as 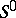 , etc. If the rank
, etc. If the rank  of the system
of the system 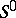 (i.e. the rank of the matrix of its coefficients) is smaller than
(i.e. the rank of the matrix of its coefficients) is smaller than 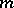 , then the
, then the  -th step will yield a system
-th step will yield a system 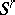 in which all coefficients at the unknowns are zero; if
in which all coefficients at the unknowns are zero; if 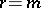 , the system is said to be empty. The system
, the system is said to be empty. The system 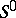 is compatible if and only if the system
is compatible if and only if the system 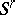 is either compatible (i.e. has no non-zero free terms) or is empty.
is either compatible (i.e. has no non-zero free terms) or is empty.
The process of obtaining one solution of a (compatible) system 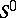 may be described as follows. One takes some solution
may be described as follows. One takes some solution 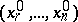 of the system
of the system  . By assigning the values
. By assigning the values  to the unknowns
to the unknowns  in some equations of the system
in some equations of the system 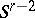 with a non-zero coefficient at
with a non-zero coefficient at 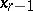 (e.g. to its first equation), one finds
(e.g. to its first equation), one finds 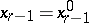 and obtains a solution
and obtains a solution 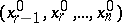 of
of 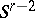 . In other words, the value
. In other words, the value 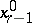 is obtained from
is obtained from 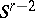 by replacing the unknowns
by replacing the unknowns  by the values taken for them. The values
by the values taken for them. The values 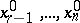 are then substituted in
are then substituted in 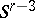 , the value
, the value 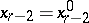 is found, and hence the solution
is found, and hence the solution 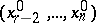 , etc. The values
, etc. The values 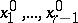 thus found, together with the values
thus found, together with the values  taken, constitute a solution
taken, constitute a solution 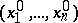 of
of 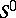 [2].
[2].
This method may be generalized as follows [4]. Let 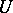 be some subspace of the vector space
be some subspace of the vector space 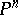 and let
and let 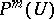 be the set of all solutions
be the set of all solutions 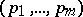 of the equation
of the equation
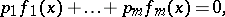 | (*) |
where  runs through
runs through 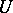 . For an arbitrary finite system
. For an arbitrary finite system
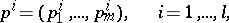 |
of non-zero generating elements of 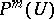 it is possible to construct a system
it is possible to construct a system
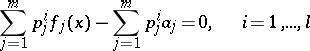 |
(where  is the unknown), known as the
is the unknown), known as the 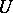 -convolution of
-convolution of 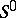 . If
. If 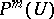 contains no non-zero elements, one says that the system
contains no non-zero elements, one says that the system 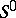 has an empty
has an empty 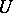 -convolution. If the system
-convolution. If the system 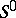 is compatible, then the
is compatible, then the 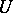 -convolution of any
-convolution of any 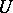 is compatible or is empty. It was found that, for the system
is compatible or is empty. It was found that, for the system 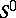 to be compatible, it is sufficient that the
to be compatible, it is sufficient that the 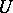 -convolution is empty or compatible for only one
-convolution is empty or compatible for only one 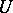 . Again, let
. Again, let 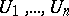 be subspaces generated in the space
be subspaces generated in the space 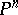 by the vectors
by the vectors 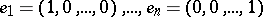 . For
. For 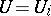 equation (*) is reduced to the equation
equation (*) is reduced to the equation
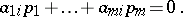 |
Let, for example, 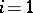 . If also
. If also 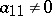 , then the vectors
, then the vectors 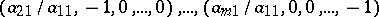 may be taken as the non-zero generating elements of the space
may be taken as the non-zero generating elements of the space 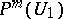 , and the
, and the 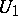 -convolution of the system
-convolution of the system 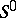 will coincide with the procedure of elimination of the unknown
will coincide with the procedure of elimination of the unknown 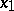 in Gauss' method.
in Gauss' method.
The 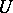 -convolution of the system
-convolution of the system 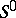 for
for  is a procedure for the simultaneous elimination of two unknowns
is a procedure for the simultaneous elimination of two unknowns 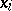 and
and 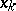 . For example, let
. For example, let 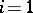 and
and 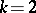 . If also
. If also
 |
then the rows of the matrix
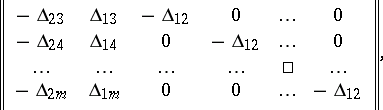 |
where
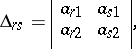 |
may be used to obtain the 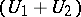 -convolution of the system
-convolution of the system 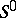 . By a suitable elimination of individual unknowns with eliminations of certain pairs (or, generally, samples) of unknowns, the system
. By a suitable elimination of individual unknowns with eliminations of certain pairs (or, generally, samples) of unknowns, the system 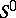 may be solved by using algorithms which are generalizations of the Gauss method.
may be solved by using algorithms which are generalizations of the Gauss method.
References
| [1] | C.F. Gauss, "Beiträge zur Theorie der algebraischen Gleichungen" , Werke , 3 , K. Gesellschaft Wissenschaft. Göttingen (1876) pp. 71–102 |
| [2] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [3] | D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian) |
| [4] | S.N. Chernikov, "Lineare Ungleichungen" , Deutsch. Verlag Wissenschaft. (1971) (Translated from Russian) |
Comments
There are a number of variants of this method, mostly based on practical implementation considerations (like the methods of Crout and Doolittle) or efficiency (like the method of Choleski for symmetric systems).
In the Western literature, the notions of LU-decomposition, forward elimination and back substitution are often associated with Gauss' method (which is also called the Gaussian elimination method). Consider the particular case where the matrix of coefficients 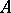 in the system
in the system 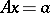 is a square matrix
is a square matrix 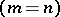 . Then LU-decomposition refers to the decomposition of
. Then LU-decomposition refers to the decomposition of 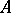 into a lower- and upper-triangular matrix
into a lower- and upper-triangular matrix 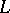 and
and 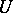 , i.e.,
, i.e., 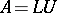 . Forward elimination and back substitution are understood to be the solution of the triangular systems
. Forward elimination and back substitution are understood to be the solution of the triangular systems 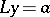 and
and 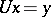 , respectively. By using the concept of a flop (as introduced by C.B. Moler), that is, the amount of work involved in performing a floating point addition, a floating point multiplication and a little subscripting, it can be shown that LU-decomposition, forward elimination and back substitution require
, respectively. By using the concept of a flop (as introduced by C.B. Moler), that is, the amount of work involved in performing a floating point addition, a floating point multiplication and a little subscripting, it can be shown that LU-decomposition, forward elimination and back substitution require 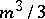 ,
, 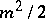 and
and 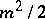 flops, respectively.
flops, respectively.
For numerical purposes it is not sufficient to ensure that the coefficients 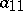 , etc., the pivots, are just non-zero, but they are the best possible; if the absolutely largest
, etc., the pivots, are just non-zero, but they are the best possible; if the absolutely largest 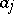 is used as a pivot, then this is called partial pivoting. If the absolutely largest element in the entire matrix (or submatrix at later stages) is used as a pivot, this is being called complete pivoting. Partial pivoting to make LU-decomposition possible in case the matrix
is used as a pivot, then this is called partial pivoting. If the absolutely largest element in the entire matrix (or submatrix at later stages) is used as a pivot, this is being called complete pivoting. Partial pivoting to make LU-decomposition possible in case the matrix 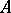 has singular leading principal submatrices amounts to interchanging rows. It requires
has singular leading principal submatrices amounts to interchanging rows. It requires 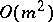 comparisons. With such a strategy the method can be shown to be numerically stable (see Stability of a computational algorithm; Stability of a computational process).
comparisons. With such a strategy the method can be shown to be numerically stable (see Stability of a computational algorithm; Stability of a computational process).
An excellent book on numerical linear algebra is [a1]. The problem of numerical stability in Gaussian elimination is discussed in [a6].
Fortan routines can be found in [a4]; for an older Algol version see [a5].
References
| [a1] | G.H. Golub, C.F. van Loan, "Matrix computations" , North Oxford Acad. (1983) |
| [a2] | J.H. Wilkinson, "The algebraic eigenvalue problem" , Clarendon Press (1965) |
| [a3] | G. Strang, "Linear algebra and its application" , Acad. Press (1976) |
| [a4] | H. Dongarra, J.R. Bunch, C.B. Moler, G.W. Stewart, "LINPACK users guide" , SIAM (1978) |
| [a5] | J.H. Wilkinson, C. Reinsch, "Handbook for automatic computation" , 2. Linear algebra , Springer (1971) |
| [a6] | P.A. Bussinger, "Monotoring the numerical stability of Gaussian elimination" Numer. Math. , 16 (1971) pp. 360–361 |
Gauss method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_method&oldid=47050