Gas flow theory

gas jet theory

The branch of gas dynamics that studies gas flows on the assumption that a part of the gas flows around an obstacle encountered in its path of propagation and runs off the obstacle while forming a zone of stagnation behind it. Problems in gas flow theory are solved on the assumption that the gas is barotropic and that its motion is plane-parallel, potential and stationary. If these conditions are met, the equations of hydrodynamics yield the fundamental formula

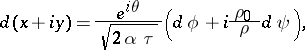(1)

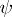in which and are, respectively, the velocity potential and the flow function, 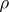is the gas density at an arbitrary point, and 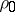is the gas density at a point where its velocity is zero. For adiabatic motions the constant 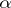is the square of the velocity of sound at the point of zero velocity of the gas divided by 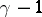, where 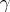is the adiabatic index. In solving problems in the theory of gas flow it is expedient to consider the unknown functions not in terms of the variables 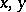(the coordinates in the plane of the flow), but rather as a function of the Chaplygin variable 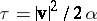and the slope angle 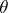made by the velocity vector with the -axis. If the independent variables are chosen in this manner, equation (1) leads to the following system of two partial differential equations:

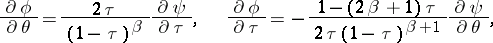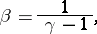to which Bernoulli's integral is to be added:

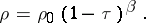Elimination of the function 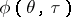leads to the following equation for the flow function:

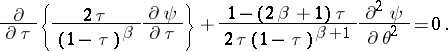(2)

This is an elliptic partial differential equation for subsonic flows and a hyperbolic partial differential equation for supersonic flows. Equation (2) may be solved for several kinds of obstacles constructed out of rectilinear segments; the variable has a corresponding constant value along each such segment. Along the flow lines, which are broken at the ends of the segments and which form the boundary between the moving gas and the gas which is at rest in the zone of stagnation, the variable has a constant value. The flow function 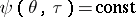at the points of the boundaries 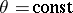and 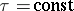. A domain bounded by the rectilinear segments parallel to the coordinate axes is formed in the plane of the variables 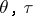; along each such segment the flow function has a constant value. The location pattern of these segments and the constant values of 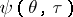on them depend on the kind and location of the obstacle in the plane of the flow of the gas. For a certain type of problem 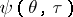may be obtained from equation (2) by separation of variables. For instance, if a gas flow of output 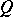and finite width encounters a rectilinear plate placed perpendicularly to the gas velocity in the remote parts of the flow, is determined by the series

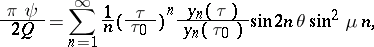(3)

where 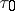is the value of the variable on the boundary line of the flow and 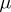is the angle formed by the velocity of the flow with the -axis at a large distance behind the plate. The angle 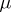may be found from the length, while the pressure exerted by the flow on the plate is found by using formula (1).

The function 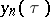is obtained by separation of variables in (2), is the integral of a hypergeometric equation,

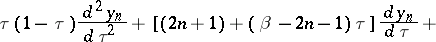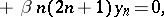and is holomorphic at .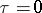

For a gas flowing out of an opening of an infinitely-wide vessel 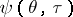is determined by the series

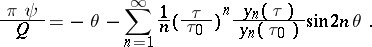(4)

The convergence of series of the type (3) and (4) was established by S.A. Chaplygin [1] for subsonic flows, i.e. for .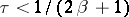

Series such as (3) and (4) for the function 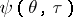may be constructed if the flow comprises only one characteristic velocity other than zero. On the other hand, if there are two or more such velocities — e.g. in the problem of gas flow from an opening in the lateral wall of the vessel bounded by two infinite straight half-lines — the solution is expressed in terms of definite integrals of a complicated structure, containing 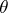and as parameters.

Chaplygin proposed an approximate method for solving problems of gas flow theory for the study of series of the type (3) and (4) and definite integrals which yield accurate solutions of the problems in the theory of gas flow. In this method the problem of gas flow is reduced to the problem of plane-parallel potential motion of an incompressible liquid.

References

[1]	S.A. Chaplygin, "On gas jets" NACA Techn. Mem. , 1063 (1944) Nauchn. Tr. Moskov. Univ. Mat. Fiz. , 21 (1904) pp. 1–121
[2]	Bai Shi-i, "The theory of jets" , Moscow (1960) (In Russian; translated from English)

References

[a1]	Y.H. Kuo, W.R. Sears, "Plane subsonic and transonic potential flows" W.R. Sears (ed.) , General theory of high speed aerodynamics , Princeton Univ. Press (1954) pp. 490–582
[a2]	A. Ferri, "Supersonic flows with shock waves" W.R. Sears (ed.) , General theory of high speed aerodynamics , Princeton Univ. Press (1954) pp. 670–748
[a3]	R. Courant, K.O. Friedrichs, "Supersonic flow and shock waves" , Interscience (1948)
[a4]	R. Hill, D.C. Pack, "An investigation, by the method of characteristics, of the lateral expansion of the gases behind a detonating slab of explosive" Proc. R. Soc. A , 191 (1947) pp. 524
[a5]	L. Bers, "Mathematical aspects of subsonic and transonic gas dynamics" , Wiley (1958)