Gamma-correlation
The two-dimensional distribution of non-negative random dependent variables 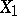 and
and 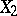 defined by the density
defined by the density
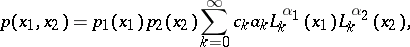 |
where
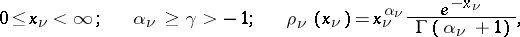 |
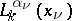 are the Laguerre polynomials, orthonormalized on the positive semi-axis with weight
are the Laguerre polynomials, orthonormalized on the positive semi-axis with weight 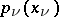 ,
, 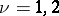 ;
;
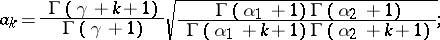 |
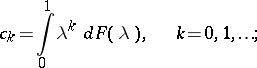 |
and 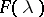 is an arbitrary distribution function on the segment
is an arbitrary distribution function on the segment  . The correlation coefficient between
. The correlation coefficient between 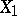 and
and  is
is 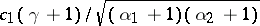 . If
. If 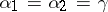 , a symmetric gamma-correlation is obtained; in such a case
, a symmetric gamma-correlation is obtained; in such a case  ,
, 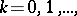 and the form of the corresponding characteristic function is
and the form of the corresponding characteristic function is
 |
If  is such that
is such that 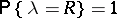 , then
, then 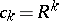 ,
, 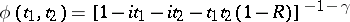 , and
, and 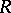 is the correlation coefficient between
is the correlation coefficient between  and
and 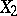 (
(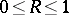 ). In this last case the density series can be summed using the formula (cf. [2]):
). In this last case the density series can be summed using the formula (cf. [2]):
 |
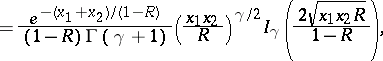 |
where 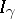 is the Bessel function of an imaginary argument [2].
is the Bessel function of an imaginary argument [2].
References
| [1] | I.O. Sarmanov, Trudy Gidrologichesk. Inst. , 162 (1969) pp. 37–61 |
| [2] | W. Myller-Lebedeff, "Die Theorie der Integralgleichungen in Anwendung auf einige Reihenentwicklungen" Math. Ann. , 64 (1907) pp. 388–416 |
Comments
This bivariate distribution is just one of the many possible multivariate generalizations of the (univariate) gamma-distribution. See [a1], Chapt. 40 for a survey as well as more details on this one.
References
| [a1] | N.L. Johnson, S. Kotz, "Distributions in statistics" , 2. Continuous multivariate distributions , Wiley (1972) |
Gamma-correlation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gamma-correlation&oldid=47037