Function of bounded characteristic
in a domain 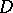 of the complex plane
of the complex plane 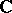
A meromorphic function 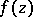 in
in 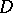 that can be represented in
that can be represented in 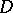 as the quotient of two bounded analytic functions,
as the quotient of two bounded analytic functions,
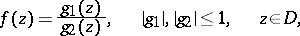 | (1) |
is called a function of bounded type. The class most studied is the class  of functions of bounded type in the unit disc
of functions of bounded type in the unit disc  : A meromorphic function
: A meromorphic function  in
in 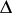 belongs to
belongs to 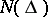 if and only if its characteristic
if and only if its characteristic 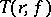 is bounded (Nevanlinna's theorem):
is bounded (Nevanlinna's theorem):
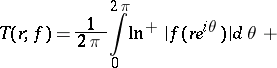 | (2) |
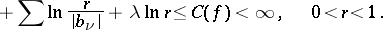 |
Here the sum on the right-hand side is taken over all poles 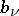 of
of 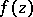 with
with 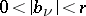 , and each pole is taken as many times as its multiplicity;
, and each pole is taken as many times as its multiplicity; 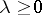 is the multiplicity of the pole at the origin. Hence functions in the class
is the multiplicity of the pole at the origin. Hence functions in the class 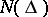 are also called functions of bounded characteristic. The following sufficient condition is also of interest: If a meromorphic function
are also called functions of bounded characteristic. The following sufficient condition is also of interest: If a meromorphic function 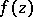 in
in 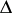 does not take a set of values
does not take a set of values 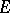 of positive capacity,
of positive capacity, 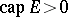 , then
, then 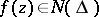 .
.
The functions 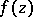 in
in 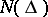 have the following properties: 1)
have the following properties: 1) 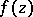 has angular boundary values
has angular boundary values 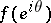 , with
, with 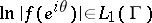 , almost-everywhere on the unit circle
, almost-everywhere on the unit circle 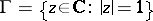 ; 2) if
; 2) if 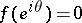 on a set of points of
on a set of points of 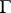 of positive measure, then
of positive measure, then 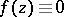 ; 3) a function
; 3) a function 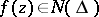 is characterized by an integral representation of the form
is characterized by an integral representation of the form
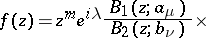 | (3) |
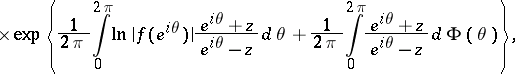 |
where 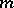 is the integer such that
is the integer such that 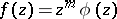 ,
, 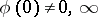 ;
; 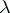 is real;
is real; 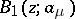 and
and 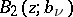 are the Blaschke products taken over all zeros
are the Blaschke products taken over all zeros 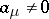 and poles
and poles 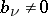 of
of 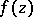 inside
inside 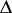 , counted with multiplicity (cf. Blaschke product); and
, counted with multiplicity (cf. Blaschke product); and 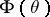 is a singular function of bounded variation on
is a singular function of bounded variation on 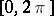 with derivative equal to zero almost-everywhere.
with derivative equal to zero almost-everywhere.
The subclass 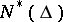 of
of 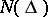 consisting of all holomorphic functions
consisting of all holomorphic functions 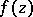 in
in 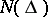 is also of interest. A necessary and sufficient condition for a holomorphic function
is also of interest. A necessary and sufficient condition for a holomorphic function 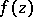 to be in
to be in 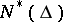 is that it satisfies the following condition, deduced from (2),
is that it satisfies the following condition, deduced from (2),
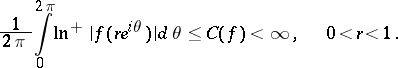 | (4) |
For 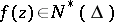 one must have
one must have 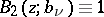 ,
, 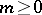 in (3).
in (3).
Condition (4) is equivalent to the requirement that the subharmonic function 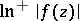 has a harmonic majorant in the whole disc
has a harmonic majorant in the whole disc 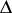 . The condition in this form is usually taken to define the class
. The condition in this form is usually taken to define the class 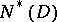 of holomorphic functions on arbitrary domains
of holomorphic functions on arbitrary domains 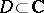 :
: 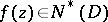 if and only if
if and only if 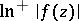 has a harmonic majorant in the whole domain
has a harmonic majorant in the whole domain 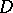 .
.
Suppose that the function 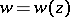 realizes a conformal universal covering mapping
realizes a conformal universal covering mapping 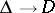 (i.e. a single-valued analytic function on
(i.e. a single-valued analytic function on 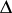 that is automorphic with respect to the group
that is automorphic with respect to the group 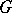 of fractional-linear transformations of the disc
of fractional-linear transformations of the disc 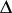 onto itself corresponding to
onto itself corresponding to 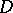 ). Then
). Then 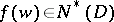 if and only if the composite function
if and only if the composite function 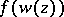 is automorphic relative to
is automorphic relative to 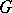 and
and 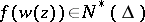 . If
. If 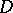 is a finitely-connected domain and if its boundary
is a finitely-connected domain and if its boundary 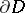 is rectifiable, then the angular boundary values
is rectifiable, then the angular boundary values 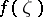 ,
, 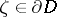 , of
, of 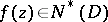 exist almost-everywhere on
exist almost-everywhere on 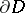 , and
, and 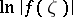 is summable with respect to harmonic measure on
is summable with respect to harmonic measure on 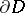 (for more details see the survey [4]).
(for more details see the survey [4]).
Now let 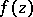 ,
, 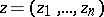 ,
, 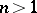 , be a holomorphic function of several variables on the unit polydisc
, be a holomorphic function of several variables on the unit polydisc 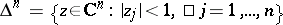 , and let
, and let 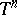 be the skeleton of
be the skeleton of  ,
, 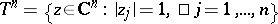 . The class
. The class 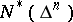 of functions of bounded characteristic is defined by a condition generalizing (4):
of functions of bounded characteristic is defined by a condition generalizing (4):
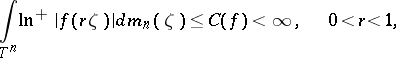 |
where 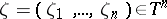 and
and 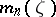 is the normalized Haar measure on
is the normalized Haar measure on 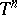 ,
, 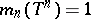 . A holomorphic function
. A holomorphic function 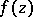 in the class
in the class 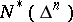 has radial boundary values
has radial boundary values 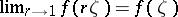 ,
, 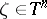 , almost-everywhere on
, almost-everywhere on 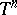 with respect to Haar measure
with respect to Haar measure 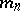 , and
, and 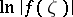 is summable on
is summable on 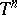 . If the original definition (1) of a function of bounded type on
. If the original definition (1) of a function of bounded type on 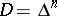 is retained, then a function
is retained, then a function 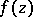 of bounded type is a function of bounded characteristic,
of bounded type is a function of bounded characteristic, 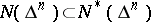 . However, for
. However, for 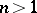 there are functions
there are functions 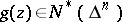 that are not representable as the quotient of two bounded holomorphic functions (see [5]).
that are not representable as the quotient of two bounded holomorphic functions (see [5]).
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | Itogi Nauk. Mat. Anal. 1963 (1965) pp. 5–80 |
| [5] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
Comments
One should not confuse the notion of "function of bounded type" as defined above with that of an entire function of bounded type. For this reason, functions 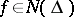 are sometimes called functions of bounded form or have no special name at all, the class
are sometimes called functions of bounded form or have no special name at all, the class 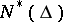 being more important.
being more important.
Function of bounded characteristic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Function_of_bounded_characteristic&oldid=47008