Frozen-in integral
The integral of the induction equation of a magnetic field for the limiting case of an ideally-conducting medium. The physical meaning of the frozen-in integral is that by moving the liquid, the force lines of the magnetic field are moved together with the liquid particles.
For the motion of an ideally-conducting medium the magnetic field strength  is described by the equation:
is described by the equation:
 |
where 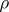 is the density and
is the density and  is the rate of motion of the medium. A change in the line element
is the rate of motion of the medium. A change in the line element 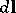 of a force line of the magnetic field is described by the equation
of a force line of the magnetic field is described by the equation
 |
The vectors  and
and 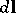 are collinear:
are collinear:
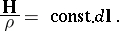 |
The following equation, which goes by the name of frozen-in integral, is valid:
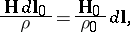 |
where the index "0" refers to the values of the parameters at the initial moment of time.
It follows from the frozen-in integral that the magnetic flux of a field across any surface, encircled by a contour of liquid particles, is independent of time.
References
| [1] | T.G. Cowling, "Magneto-hydrodynamics" , Interscience (1957) |
| [2] | L.D. Landau, E.M. Lifshitz, "Electrodynamics of continous media" , Pergamon (1960) (Translated from Russian) |
| [3] | A.G. Kulikovskii, G.A. Lyubimov, "Magnetic hydrodynamics" , Moscow (1962) (In Russian) |
Frozen-in integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frozen-in_integral&oldid=46996