Frequency theorem

A theorem that states conditions for the solvability of the Lur'e equations in control theory:

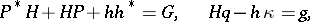(1)

where 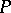, , 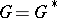, , 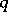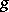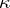are given , , , , and matrices respectively, and 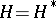, 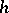are the required and 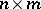matrices. The Lur'e equations have two other equivalent forms: If ,

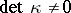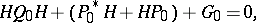(2)

where 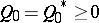, , and in the general case

(3)

where 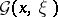is a given Hermitian form of two vectors , ;

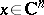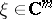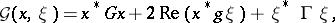Moreover, , , , .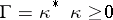

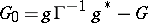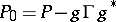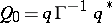Let the pair 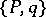be controllable: . Then the Lur'e equations reduce to the case where

If and all the matrices are real, the Lur'e equations in scalar notation take the form

here is the required vector.

The frequency theorem asserts that for the Lur'e equations to be solvable it is necessary and sufficient that

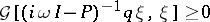for all 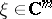, , 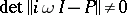( 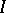is the identity matrix). The frequency theorem also formulates a procedure for determining the matrices 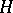and 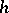and asserts that if

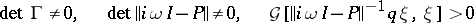(for all , and all 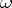), then there exist (unique) matrices and 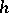such that (except for the case of equation (3)) the following is true: is a Hurwitz matrix (see [3]).

The Lur'e equations in the form (2) are also sometimes called the matrix algebraic Riccati equation. The frequency theorem is used when solving problems on absolute stability [2], [4]–[6], control and adaptation (see, for example, [7]–[9]).

References

[1]	A.I. Lur'e, "Some non-linear problems of the theory of automatic control" , Moscow-Leningrad (1951) (In Russian)
[2]	V.M. Popov, "Hyperstability of control systems" , Springer (1973) (Translated from Rumanian)
[3]	V.A. Yakubovich, "A frequency theorem in control theory" Sib. Math. J. , 14 : 2 (1973) pp. 265–289 Sibirsk. Mat. Zh. , 14 : 2 (1973) pp. 384–420
[4]	A.K. Gelig, G.A. Leonov, V.A. Yakubovich, "Stability of non-linear systems with a unique equilibrium state" , Moscow (1978) (In Russian)
[5]	, Methods for studing non-linear systems of automatic control , Moscow (1975) (In Russian)
[6]	D.D. Siljak, "Nonlinear systems. Parameter analysis and design" , Wiley (1969)
[7]	V.N. Fomin, A.L. Fradkov, V.A. Yakubovich, "Adaptive control of dynamic objects" , Moscow (1981) (In Russian)
[8a]	J.C. Willems, "Almost invariant subspaces: an approach to high gain feedback design I. Almost controlled invariant subspaces" IEEE Trans. Autom. Control , 1 (1981) pp. 235–252
[8b]	J.C. Willems, "Almost invariant subspaces: an approach to high gain feedback design I. Almost conditionally invariant subspaces" IEEE Trans. Autom. Control , 5 (1982) pp. 1071–1084
[9]	W. Coppel, "Matrix quadratic equations" Bull. Austr. Math. Soc. , 10 (1974) pp. 377–401

Comments

The frequency theorem is better known as the Kalman–Yakubovich lemma or Kalman–Yacubovich lemma.

References

[a1]	R.E. Kalman, "Lyapunov functions for the problem of Lurie in automatic control" Proc. Nat. Acad. Soc. USA , 49 : 2 (1963) pp. 201–205
[a2]	B.D.O. Anderson, S. Vongpanitlerd, "Network analysis and synthesis: a modern systems theory approach" , Prentice-Hall (1973)