Free set

in a vector space 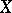over a field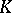

A linearly independent system of vectors from 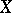, that is, a set of elements 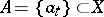, , 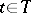such that the relation 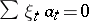, where 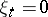for all but a finite number of indices 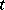, implies that 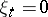for all 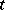. A non-free set is also called dependent.

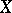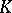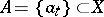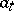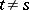A free set in a topological vector space over a field (a topologically-free set) is a set such that for any the closed subspace generated by the points , , does not contain 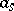. A topologically-free set is a free set in the vector space; the converse is not true. For example, in the normed space 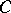of continuous functions on 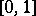, the functions 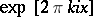, , form a topologically-free set, in contrast to the functions 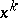(since, e.g., is contained in the closed subspace generated by ).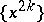

The set of all (topologically-) free sets in 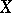is, in general, not inductive under inclusion; in addition, it does not necessarily contain a maximal topologically-free set. For example, let 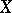be the space over 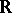formed by the continuous functions and endowed with the following Hausdorff topology: a fundamental system of neighbourhoods of zero in 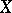consists of the balanced absorbing sets 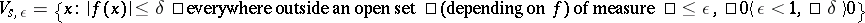. Then every continuous linear functional vanishes, and 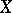does not contain a maximal free set.

For 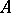to be a (topologically-) free set in the weak topology 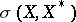in 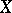it is necessary and sufficient that for each 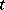there is a 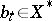such that , and 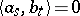for all 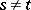. For a locally convex space a free set in the weak topology is a free set in the original topology.