Free product of groups
, 
A group 
generated by the groups 
such that any homomorphisms 
of the 
into an arbitrary group 
can be extended to a homomorphism 
. The symbol * is used to denote a free product, for example,
 |
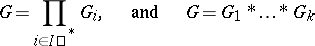in the case of a finite set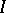 
. Each element of a free product 
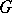that is not the identity can be expressed uniquely as an irreducible word 
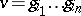, where 
, 
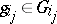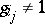and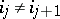 
for any 
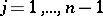. The construction of a free product is important in the study of groups defined by a set of generating elements and defining relations. In these terms it can be defined as follows. Suppose that each group 
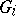is defined by sets 
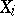of generators and 
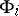of defining relations, where 
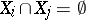if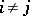 
. Then the group 
defined by the set 
of generators and the set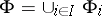 
of defining relations is the free product of the groups 
, 
.
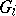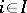Every subgroup of a free product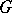 
can be decomposed into a free product of subgroups, of which some are infinite cyclic and each of the others is conjugate with some subgroup of a group 
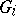in the free decomposition of 
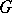(Kurosh' theorem).
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [2] | W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations in terms of generators and relations" , Wiley (Interscience) (1966) |
Comments
The notion of a free product of groups is a special case of that of a free product with amalgamated subgroup (see Amalgam of groups).
Free product of groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_product_of_groups&oldid=46986