Free ideal ring
fir.
A (non-commutative) ring (with unit element) in which all (one-sided) ideals are free. More precisely, a right fir is a ring 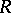 in which all right ideals are free of unique rank, as right
in which all right ideals are free of unique rank, as right 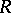 -modules. A left fir is defined correspondingly. Firs may be regarded as generalizing the notion of a principal ideal domain.
-modules. A left fir is defined correspondingly. Firs may be regarded as generalizing the notion of a principal ideal domain.
Consider dependence relations of the form  ,
, 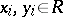 (
( a row vector,
a row vector, 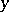 a column vector). Such a relation is called trivial if for each
a column vector). Such a relation is called trivial if for each 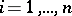 either
either  or
or 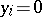 . An
. An  -term relation
-term relation 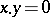 is trivialized by an invertible
is trivialized by an invertible 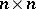 matrix
matrix 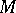 if the relation
if the relation 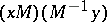 is trivial. Now let
is trivial. Now let 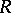 be a non-zero ring with unit element, then the following properties are all equivalent: i) every
be a non-zero ring with unit element, then the following properties are all equivalent: i) every 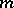 -term relation
-term relation 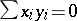 ,
, 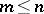 , can be trivialized by an invertible
, can be trivialized by an invertible 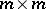 matrix; ii) given
matrix; ii) given 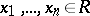 ,
, 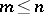 , which are right linearly dependent, there exist
, which are right linearly dependent, there exist 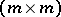 -matrices
-matrices 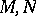 such that
such that 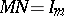 and
and 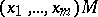 has at least one zero component; iii) any right ideal of
has at least one zero component; iii) any right ideal of 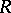 generated by
generated by 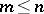 right linearly dependent elements has fewer than
right linearly dependent elements has fewer than 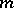 generators; and iv) any right ideal of
generators; and iv) any right ideal of 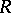 on at most
on at most  generators is free of unique rank. These properties are also equivalent to their left-right analogues. There are several more equivalent conditions, cf. [a1].
generators is free of unique rank. These properties are also equivalent to their left-right analogues. There are several more equivalent conditions, cf. [a1].
A ring which satisfies these conditions is called an  -fir. A ring which is an
-fir. A ring which is an  -fir for all
-fir for all  is called a semi-fir.
is called a semi-fir.
An integral domain 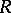 satisfying
satisfying 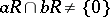 for all
for all 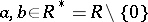 (the Ore condition) is called a right Ore ring (cf. also Associative rings and algebras for Ore's theorem). It follows that a ring
(the Ore condition) is called a right Ore ring (cf. also Associative rings and algebras for Ore's theorem). It follows that a ring 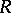 is a Bezout domain (cf. Bezout ring) if and only if it is a
is a Bezout domain (cf. Bezout ring) if and only if it is a  -fir and a right Ore ring.
-fir and a right Ore ring.
For any ring 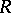 the following are equivalent: 1)
the following are equivalent: 1) 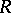 is a total matrix ring over a semi-fir; 2)
is a total matrix ring over a semi-fir; 2) 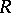 is Morita equivalent (cf. Morita equivalence) to a semi-fir; 3)
is Morita equivalent (cf. Morita equivalence) to a semi-fir; 3) 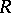 is right semi-hereditary (i.e. all finitely-generated right ideals are projective) and
is right semi-hereditary (i.e. all finitely-generated right ideals are projective) and 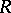 is projective-trivial; and 4) the left-right analogue of 3). Here a ring is projective-trivial if there exists a projective right module
is projective-trivial; and 4) the left-right analogue of 3). Here a ring is projective-trivial if there exists a projective right module 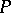 (called the minimal projective of
(called the minimal projective of 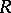 ) such that every finitely-projective right module
) such that every finitely-projective right module 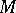 is the direct sum of
is the direct sum of  copies of
copies of 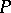 for some
for some  unique determined by
unique determined by 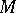 .
.
For any ring 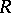 the following are equivalent: a)
the following are equivalent: a) 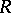 is a total matrix ring over a right fir; b)
is a total matrix ring over a right fir; b) 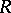 is Morita equivalent to a right fir; and c)
is Morita equivalent to a right fir; and c) 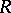 is right hereditary (i.e. all right ideals are projective) and projective-trivial.
is right hereditary (i.e. all right ideals are projective) and projective-trivial.
If 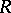 is a semi-fir, then a right module
is a semi-fir, then a right module  is flat if and only if every finitely-generated submodule of
is flat if and only if every finitely-generated submodule of 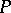 is free (i.e. if and only if
is free (i.e. if and only if 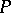 is locally free).
is locally free).
References
| [a1] | P.M. Cohn, "Free rings and their relations" , Acad. Press (1971) |
Free ideal ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_ideal_ring&oldid=46985