Fractional-linear function
A function of the type
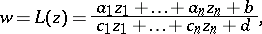 |
where 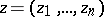 are complex or real variables,
are complex or real variables, 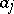 ,
, 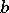 ,
, 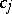 ,
, 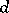 are complex or real coefficients, and
are complex or real coefficients, and 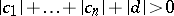 . If
. If  , the fractional-linear function is an integral-linear function; if the rank of the matrix
, the fractional-linear function is an integral-linear function; if the rank of the matrix
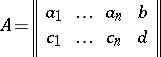 |
is equal to one,  is a constant. A proper fractional-linear function is obtained if
is a constant. A proper fractional-linear function is obtained if 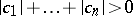 and if the rank of
and if the rank of 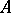 is two; it assumed in what follows that these conditions have been met.
is two; it assumed in what follows that these conditions have been met.
If 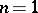 and
and 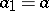 ,
, 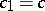 ,
, 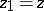 are real, the graph of the fractional-linear function is an equilateral hyperbola with the asymptotes
are real, the graph of the fractional-linear function is an equilateral hyperbola with the asymptotes 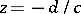 and
and 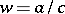 . If
. If 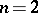 and
and 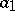 ,
, 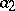 ,
, 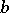 ,
, 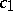 ,
, 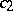 ,
, 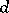 ,
, 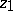 ,
, 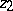 are real, the graph of the fractional-linear function is hyperbolic paraboloid.
are real, the graph of the fractional-linear function is hyperbolic paraboloid.
If 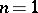 , the fractional-linear function
, the fractional-linear function 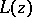 is an analytic function of the complex variable
is an analytic function of the complex variable  everywhere in the extended complex plane
everywhere in the extended complex plane 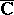 , except at the point
, except at the point 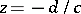 at which
at which 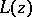 has a simple pole. If
has a simple pole. If 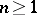 , the fractional-linear function
, the fractional-linear function 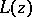 is a meromorphic function in the space
is a meromorphic function in the space 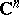 of the complex variable
of the complex variable 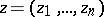 , with the set
, with the set
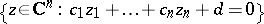 |
as its polar set.
See also Fractional-linear mapping.
Fractional-linear function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractional-linear_function&oldid=46967