Forking
(in logic)
A notion introduced by S. Shelah [a8]. The general theory of forking is also known as stability theory, but more commonly, non-forking (the negation of forking) is defined as a certain well-behaved relation between a type and its extension (cf. Types, theory of).
Let 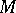 be a sufficiently saturated model of a theory
be a sufficiently saturated model of a theory 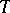 in a countable first-order language (cf. also Formal language; Model (in logic); Model theory). Given an
in a countable first-order language (cf. also Formal language; Model (in logic); Model theory). Given an  -tuple of variables
-tuple of variables 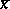 and
and 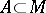 , a collection of formulas
, a collection of formulas 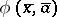 with parameters
with parameters 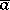 in
in 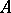 is called an
is called an  -type over
-type over 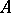 . For simplicity, only
. For simplicity, only 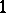 -types will be considered; these are simply called types over
-types will be considered; these are simply called types over 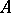 . A complete type is one which is maximal consistent. Let
. A complete type is one which is maximal consistent. Let 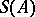 be the set of complete types over
be the set of complete types over 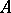 .
.
Given a type 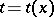 and a formula
and a formula 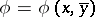 , one defines the Morley
, one defines the Morley 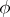 -rank of
-rank of 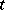 ,
, 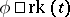 , inductively as follows:
, inductively as follows: 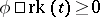 if
if 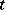 is consistent, for each natural number
is consistent, for each natural number  ,
, 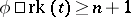 if for every finite
if for every finite 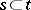 and natural number
and natural number 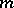 there are collections
there are collections 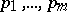 of
of 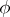 -formulas (with parameters from
-formulas (with parameters from 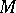 ) such that:
) such that:
i) for 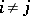 ,
, 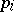 and
and 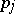 are contradictory, i.e. for some
are contradictory, i.e. for some 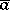 ,
, 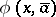 belongs to one of
belongs to one of 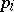 and
and 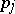 , and
, and 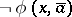 belongs to the other;
belongs to the other;
ii) 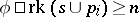 .
.
Assume that 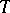 is stable, i.e. for some infinite
is stable, i.e. for some infinite 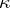 , whenever
, whenever 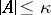 , then also
, then also  . (Equivalently,
. (Equivalently, 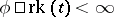 for every type
for every type 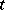 and formula
and formula 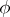 .) Let
.) Let 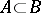 ,
, 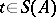 ,
, 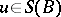 be such that
be such that 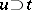 . Then
. Then  is called a non-forking extension of
is called a non-forking extension of 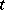 , or it is said that
, or it is said that  does not fork over
does not fork over 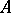 , if for every formula
, if for every formula 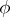 with
with 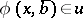 ,
,
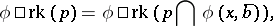 |
where  denotes the set
denotes the set 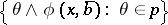 .
.
Let  mean that
mean that  is a non-forking extension of
is a non-forking extension of 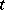 . Then
. Then  is the unique relation on complete types satisfying the following Lascar axioms:
is the unique relation on complete types satisfying the following Lascar axioms:
1)  is preserved under automorphisms of
is preserved under automorphisms of  ;
;
2) if 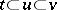 , then
, then  if and only if
if and only if  and
and  ;
;
3) for any 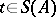 and
and 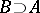 there exists a
there exists a 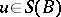 such that
such that  ;
;
4) for any  there exist countable
there exist countable 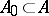 and
and 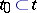 , where
, where 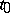 is the restriction of
is the restriction of  to formulas with parameters from
to formulas with parameters from 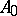 ;
;
5) for any  and
and 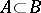 ,
,
 |
The ultrapower construction (cf. also Ultrafilter) gives a systematic way of building non-forking extensions [a4].
For  one writes
one writes 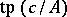 for the type in
for the type in 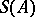 realized by
realized by  . Given a set
. Given a set 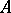 and
and 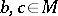 , the following important symmetry property holds:
, the following important symmetry property holds: 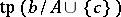 does not fork over
does not fork over  if and only if
if and only if 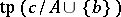 does not fork over
does not fork over 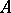 . If either holds, one says that
. If either holds, one says that 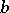 ,
,  are independent over
are independent over 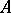 , and this notion is viewed as a generalization of algebraic independence.
, and this notion is viewed as a generalization of algebraic independence.
Given 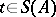 ,
, 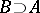 ,
, 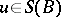 , and
, and 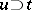 , one says that
, one says that  is an heir of
is an heir of 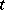 if for every
if for every 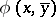 (with parameters in
(with parameters in 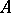 ),
), 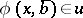 for some
for some 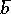 in
in 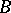 if and only if
if and only if 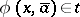 for some
for some 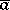 in
in  . One says that
. One says that  is definable over
is definable over 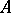 if for every
if for every 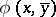 there is a formula
there is a formula 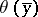 with parameters from
with parameters from 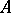 such that for any
such that for any 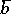 in
in 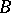 ,
, 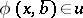 if and only if
if and only if 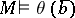 .
.
 is said to be a coheir of
is said to be a coheir of 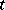 if
if  is finitely satisfiable in
is finitely satisfiable in 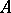 . So, for
. So, for 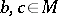 ,
, 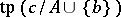 is an heir of
is an heir of 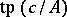 if and only if
if and only if 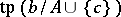 is a coheir of
is a coheir of 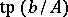 .
.
If 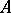 is an elementary submodel of
is an elementary submodel of 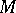 , then
, then  if and only if
if and only if  is an heir of
is an heir of 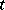 if and only if
if and only if  is definable over
is definable over 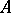 . In particular, in that case
. In particular, in that case 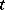 has a unique non-forking extension over any
has a unique non-forking extension over any 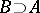 . Then it follows from the forking symmetry that when
. Then it follows from the forking symmetry that when 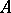 is an elementary submodel,
is an elementary submodel, 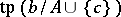 being a coheir of
being a coheir of 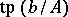 is equivalent to being an heir.
is equivalent to being an heir.
For a comprehensive introduction of forking see [a1], [a2], [a4], [a5], and [a9]. For applications in algebra, see [a7] and [a6].
The techniques of forking have been extended to unstable theories. In [a2], this is done by considering only types that satisfy stable conditions. In [a3], types are viewed as probability measures and forking is treated as a special kind of measure extension. The stability assumption is then weakened to theories that do not have the independence property.
References
| [a1] | J.T. Baldwin, "Fundamentals of stability theory" , Springer (1987) |
| [a2] | V. Harnik, L. Harrington, "Fundamentals of forking" Ann. Pure and Applied Logic , 26 (1984) pp. 245–286 |
| [a3] | H.J. Keisler, "Measures and forking" Ann. Pure and Applied Logic , 34 (1987) pp. 119–169 |
| [a4] | D. Lascar, B. Poizat, "An introduction to forking" J. Symb. Logic , 44 (1979) pp. 330–350 |
| [a5] | A. Pillay, "Introduction to stability theory" , Oxford Univ. Press (1983) |
| [a6] | A. Pillay, "The geometry of forking and groups of finite Morley rank" J. Symb. Logic , 60 (1995) pp. 1251–1259 |
| [a7] | M. Prest, "Model theory and modules" , Cambridge Univ. Press (1988) |
| [a8] | S. Shelah, "Classification theory and the number of non-isomorphic models" , North-Holland (1990) (Edition: Revised) |
| [a9] | M. Makkai, "A survey of basic stability theory" Israel J. Math. , 49 (1984) pp. 181–238 |
Forking. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Forking&oldid=46953