Folium of Descartes

A plane algebraic curve of order three which is given in Cartesian coordinates by the equation 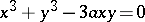; the parametric equations are

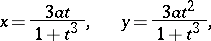where 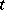is the tangent of the angle between the radius vector of the curve and the -axis. The folium of Descartes is symmetric about the axis (see Fig.). The tangent lines are parallel to the coordinate axes at the points with coordinates 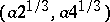and 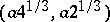. The coordinate origin is a nodal point with the coordinate axes as tangent lines. The asymptote is given by 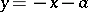. The surface area enclosed between the curve and the asymptote is 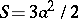. The surface area of the loop is 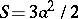. Named after R. Descartes who was the first to study it in 1638.

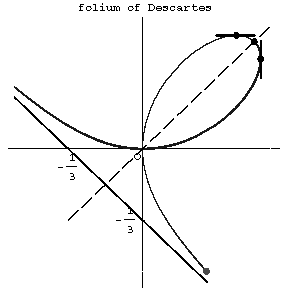
Figure: f040750a

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)
[2]	A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)

References

[a1]	J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)
[a2]	K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962)