Finite group scheme
A group scheme that is finite and flat over the ground scheme. If 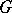 is a finite group scheme over a scheme
is a finite group scheme over a scheme 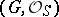 , then
, then 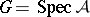 , where
, where 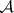 is a finite flat quasi-coherent sheaf of algebras over
is a finite flat quasi-coherent sheaf of algebras over 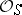 . From now on it is assumed that
. From now on it is assumed that 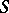 is locally Noetherian. In this case
is locally Noetherian. In this case 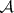 is locally free. If
is locally free. If 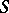 is connected, then the rank of
is connected, then the rank of 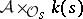 over the field of residues
over the field of residues 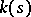 at a point
at a point 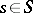 is independent of
is independent of  and is called the rank of the finite group scheme. Let
and is called the rank of the finite group scheme. Let  be the morphism of
be the morphism of 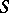 -schemes mapping an element
-schemes mapping an element 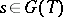 into
into 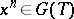 , where
, where 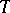 is an arbitrary
is an arbitrary 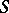 -scheme. The morphism
-scheme. The morphism 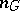 is null if the rank of
is null if the rank of 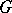 divides
divides  and if
and if 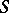 is a reduced scheme or if
is a reduced scheme or if 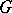 is a commutative finite group scheme (see Commutative group scheme). Every finite group scheme of rank
is a commutative finite group scheme (see Commutative group scheme). Every finite group scheme of rank 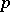 , where
, where 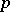 is a prime number, is commutative [2].
is a prime number, is commutative [2].
If 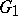 is a subgroup of a finite group scheme
is a subgroup of a finite group scheme 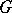 , then one can form the finite group scheme
, then one can form the finite group scheme 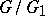 , and the rank of
, and the rank of 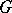 is the product of the ranks of
is the product of the ranks of 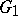 and
and 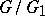 .
.
Examples.
1) Let 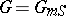 be a multiplicative group scheme (or Abelian scheme
be a multiplicative group scheme (or Abelian scheme 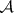 over
over 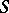 ); then
); then 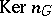 is a finite group scheme of rank
is a finite group scheme of rank 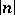 (or
(or 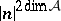 ).
).
2) Let 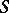 be a scheme over the prime field
be a scheme over the prime field 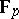 and let
and let 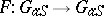 be the Frobenius homomorphism of the additive group scheme
be the Frobenius homomorphism of the additive group scheme 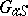 . Then
. Then 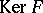 is a finite group scheme of rank
is a finite group scheme of rank 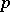 .
.
3) For every abstract finite group scheme 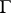 of order
of order  the constant group scheme
the constant group scheme 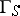 is a finite group scheme of rank
is a finite group scheme of rank  .
.
The classification of finite group schemes over arbitrary ground schemes has been achieved in the case where the rank of 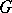 is a prime number (cf. [2]). The case where
is a prime number (cf. [2]). The case where 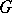 is a commutative finite group scheme and
is a commutative finite group scheme and 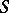 is the spectrum of a field of characteristic
is the spectrum of a field of characteristic 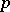 is well known (see [1], [3], [7]).
is well known (see [1], [3], [7]).
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 (1963) pp. 1–80 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 |
| [2] | J. Tate, F. Oort, "Group schemes of prime order" Ann. Sci. Ecole Norm. Sup. , 3 (1970) pp. 1–21 |
| [3] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970) |
| [4] | F. Oort, "Commutative group schemes" , Lect. notes in math. , 15 , Springer (1966) |
| [5] | S. Shatz, "Cohomology of Artinian group schemes over local fields" Ann. of Math. , 79 (1964) pp. 411–449 |
| [6] | B. Mazur, "Notes on étale cohomology of number fields" Ann. Sci. Ecole Norm. Sup. , 6 (1973) pp. 521–556 |
| [7] | H. Kraft, "Kommutative algebraische Gruppen und Ringe" , Springer (1975) |
Comments
For some spectacular applications of the results in [a1] see [a2], [a3].
References
| [a1] | M. Raynaud, "Schémas en groupes de type 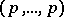 " Bull. Soc. Math. France , 102 (1974) pp. 241–280 " Bull. Soc. Math. France , 102 (1974) pp. 241–280 |
| [a2] | J.-M. Fontaine, "Il n'y a pas de variété abélienne sur  " Invent. Math. , 81 (1985) pp. 515–538 " Invent. Math. , 81 (1985) pp. 515–538 |
| [a3] | G. Faltings, "Endlichkeitssätze für abelsche Varietäten über Zahlkörpern" Invent. Math. , 73 (1983) pp. 349–366 (Erratum: Invent. Math 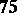 (1984), 381) (1984), 381) |
| [a4] | G. Cornell (ed.) J. Silverman (ed.) , Arithmetic geometry , Springer (1986) |
Finite group scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite_group_scheme&oldid=46929