Filtered algebra
An algebra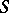 
in which there are distinguished subspaces 
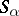, indexed by the elements of a totally ordered group 
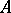(most often 
is the additive group of integers 
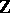), such that 
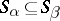for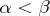 
and 
(an increasing filtration). Sometimes one considers the case where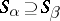 
for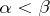 
(a decreasing filtration), but it reduces to the preceding case by reversing the order in 
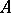. With each filtered algebra 
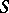one associates the graded algebra
 |
where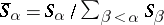 
(if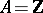 
, then 
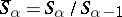), and the product of the elements 
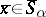and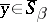 
is defined by the formula 
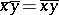, where 
and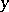 
are representatives of the cosets 
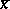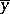and 
, and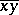 
is the coset of 
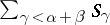generated by 
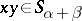. If some multilinear identity is satisfied in 
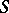(for example, commutativity, associativity, or the Jacobi identity), then it is also satisfied in 
.
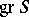Examples.
1) Let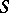 
be a Clifford algebra and let 
, 
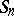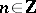, be the collection of elements that can be represented in the form of (non-commutative) polynomials of degree 
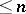in the generators. One obtains an increasing 
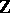-filtration of 
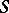in which 
for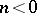 
. The associated graded algebra is the exterior algebra with the same number of generators.
2) In the universal enveloping algebra of a Lie algebra one can define an increasing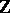 
-filtration in the same way as in the preceding example. By the Birkhoff–Witt theorem, the associated graded algebra is the polynomial algebra.
Filtered algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Filtered_algebra&oldid=46920