Feynman measure

A complex pre-measure defined on cylindrical sets in the space of functions 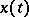, , 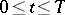, 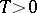with values in 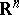, by the formula

(1)

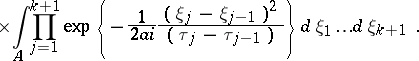Here 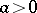is a parameter, 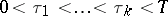, and

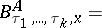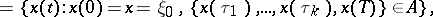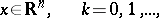where 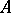is some Borel subset in 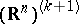. Sometimes one also considers the so-called conditional Feynman measure 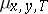obtained from the measure (1) by restricting it to the set of trajectories with "end" at the point 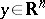: 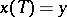. The measure 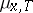, and also 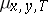, was introduced by R.P. Feynman in connection with representing the semi-group 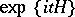, where 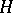is a Sturm–Liouville operator, in the form of a path integral — a Feynman integral.

References

[1]	R.P. Feynman, "Space-time approach to non-relativistic quantum mechanics" Rev. Modern Phys. , 20 (1948) pp. 367–387
[2]	Yu.L. Daletskii, "Integration in function spaces" Progress in Mathematics , 4 (1969) pp. 87–132 Itogi Nauk. Mat. Anal. 1966 (1967) pp. 83–124
[3]	S.A. Albeverio, R.J. Høegh-Krohn, "Mathematical theory of Feynman path integrals" , Springer (1976)