Favard inequality

The inequality

(*)

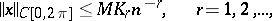where

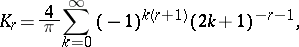and the function 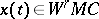is orthogonal to every trigonometric polynomial of order not exceeding 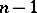. For 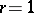inequality (*) was proved by H. Bohr (1935), so it is also called the Bohr inequality and the Bohr–Favard inequality. For an arbitrary positive integer inequality (*) was proved by J. Favard [1].

References

[1]	J. Favard, "Sur l'approximation des fonctions périodiques par des polynomes trigonométriques" C.R. Acad. Sci. Paris , 203 (1936) pp. 1122–1124
[2]	V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian)

Comments

For a definition of the space 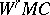cf. Favard problem.