Faithful functor

A functor which is "injective on Hom-sets" . Explicitly, a functor is called faithful if, given any two morphisms in with the same domain and codomain, the equation implies . The name derives from the representation theory of groups: a permutation (respectively, -linear) representation of a group is faithful if and only if it is faithful when considered as a functor (respectively ). A faithful functor reflects monomorphisms (that is, monic implies monic) and epimorphisms; hence if the domain category 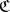is balanced (i.e. has the property that any morphism which is both monic and epic is an isomorphism) then it also reflects isomorphisms. A functor with the latter property is generally called conservative; however, some authors include this condition in the definition of faithfulness.

In Russian literature there seems to be some confusion between the terms "faithful functor" and "exact functor" , see also Exact functor.

References

[a1]	B. Mitchell, "Theory of categories" , Acad. Press (1965)