Factorization theorem
factorization criterion
A theorem in the theory of statistical estimation giving a necessary and sufficient condition for a statistic 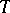 to be sufficient for a family of probability distributions
to be sufficient for a family of probability distributions 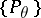 (cf. Sufficient statistic).
(cf. Sufficient statistic).
Let 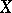 be a random vector taking values in a sample space
be a random vector taking values in a sample space 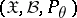 ,
, 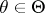 , where the family of probability distributions
, where the family of probability distributions 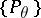 is dominated by some measure
is dominated by some measure 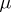 , and let
, and let
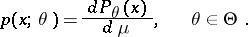 |
Further, let 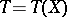 be a statistic constructed from the observation vector of
be a statistic constructed from the observation vector of 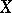 and mapping the measurable space
and mapping the measurable space 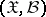 into the measurable space
into the measurable space 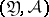 . Under these conditions the following question arises: When is
. Under these conditions the following question arises: When is 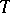 sufficient for the family
sufficient for the family 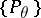 ? As an answer to this question, the factorization theorem asserts: For a statistic
? As an answer to this question, the factorization theorem asserts: For a statistic  to be sufficient for a family
to be sufficient for a family 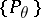 that admits sufficient statistics, it is necessary and sufficient that for every
that admits sufficient statistics, it is necessary and sufficient that for every 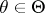 the probability density
the probability density 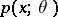 can be factorized in the following way:
can be factorized in the following way:
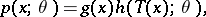 | (*) |
where 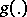 is a
is a  -measurable function on
-measurable function on 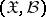 , and
, and 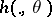 is an
is an 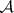 -measurable function on
-measurable function on 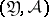 . The factorization theorem, beyond giving a criterion for sufficiency, in many cases enables one to determine the concrete form of the sufficient statistic
. The factorization theorem, beyond giving a criterion for sufficiency, in many cases enables one to determine the concrete form of the sufficient statistic 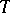 for which the density
for which the density 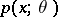 must factorize by the formula (*). In practice it is usually preferable to deal with the likelihood function
must factorize by the formula (*). In practice it is usually preferable to deal with the likelihood function 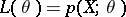 rather than with the density
rather than with the density 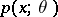 . In terms of the likelihood function the condition (*) has the form
. In terms of the likelihood function the condition (*) has the form 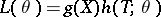 , explicitly containing
, explicitly containing 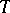 .
.
References
| [1] | R.A. Fischer, "On the mathematical foundations of theoretical statistics" Philos. Trans. Roy. Soc. London Ser. A , 222 (1922) pp. 309–368 |
| [2] | J. Neyman, "Su un teorema concernente le cosiddette statistiche sufficienti" Giorn. Istit. Ital. Att. , 6 (1935) pp. 320–334 |
| [3] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959) |
| [4] | I.A. Ibragimov, R.Z. [R.Z. Khas'minskii] Has'minskii, "Statistical estimation: asymptotic theory" , Springer (1981) (Translated from Russian) |
| [5] | P.R. Halmos, L.J. Savage, "Application of the Radon–Nikodym theorem to the theory of sufficient statistics" Ann. of Math. Statist. , 20 (1949) pp. 225–241 |
Comments
References
| [a1] | D.R. Cox, D.V. Hinkley, "Theoretical statistics" , Chapman & Hall (1974) pp. 21 |
Factorization theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Factorization_theorem&oldid=46900