FKG inequality
From Encyclopedia of Mathematics
Fortuin–Kasteleyn–Ginibre inequality
An inequality [a3] that began a series of correlation inequalities for finite partially ordered sets. Let  be a finite partially ordered set ordered by
be a finite partially ordered set ordered by  (irreflexive, transitive) with
(irreflexive, transitive) with  a distributive lattice:
a distributive lattice:  ,
,  , and
, and  for all
for all  . Suppose
. Suppose  is log supermodular:
is log supermodular:
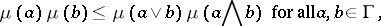 |
and that  and
and  are non-decreasing:
are non-decreasing:
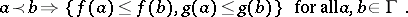 |
The FKG inequality is:
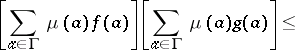 |
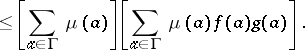 |
If 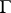 is a Boolean algebra and
is a Boolean algebra and  is a probability measure on
is a probability measure on  , the inequality is
, the inequality is  , where
, where 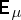 denotes mathematical expectation.
denotes mathematical expectation.
Related inequalities are discussed in [a1], [a2], [a4], [a5], [a6], [a7], [a8], [a9].
See also Ahlswede–Daykin inequality; Fishburn–Shepp inequality; Holley inequality.
References
| [a1] | B. Bollobás, "Combinatorics" , Cambridge Univ. Press (1986) |
| [a2] | P.C. Fishburn, "Correlation in partially ordered sets" Discrete Appl. Math. , 39 (1992) pp. 173–191 |
| [a3] | C.M. Fortuin, P.N. Kasteleyn, J. Ginibre, "Correlation inequalities for some partially ordered sets" Comm. Math. Phys. , 22 (1971) pp. 89–103 |
| [a4] | R.L. Graham, "Linear extensions of partial orders and the FKG inequality" I. Rival (ed.) , Ordered sets , Reidel (1982) pp. 213–236 |
| [a5] | R.L. Graham, "Applications of the FKG inequality and its relatives" , Proc. 12th Internat. Symp. Math. Programming , Springer (1983) pp. 115–131 |
| [a6] | R. Holley, "Remarks on the FKG inequalities" Comm. Math. Phys. , 36 (1974) pp. 227–231 |
| [a7] | K. Joag-Dev, L.A. Shepp, R.A. Vitale, "Remarks and open problems in the area of the FKG inequality" , Inequalities Stat. Probab. , IMS Lecture Notes , 5 (1984) pp. 121–126 |
| [a8] | L.A. Shepp, "The XYZ conjecture and the FKG inequality" Ann. of Probab. , 10 (1982) pp. 824–827 |
| [a9] | P M. Winkler, "Correlation and order" Contemp. Math. , 57 (1986) pp. 151–174 |
How to Cite This Entry:
FKG inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=FKG_inequality&oldid=46896
FKG inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=FKG_inequality&oldid=46896
This article was adapted from an original article by P.C. Fishburn (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article