Extension theorems (in analytic geometry)

Statements on the continuation (extension) of functions, sections of analytic sheaves, analytic sheaves, analytic subsets, holomorphic and meromorphic mappings, from the complement 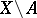in an analytic space 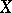of a set 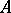(as a rule, also analytic) to the whole space 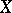. Two theorems of B. Riemann form the classical results concerning continuation of functions.

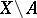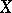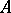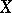Riemann's first theorem states that every analytic function on , where is a normal complex space and an analytic subspace of codimension , can be continued to an analytic function on . Riemann's second theorem states that every analytic functi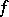on on 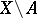that is locally bounded on 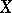, where 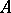is a nowhere-dense analytic subset in a normal complex space 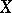, can be continued to an analytic function on 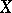. There are generalizations of these theorems to arbitrary complex spaces , as well as to sections of coherent analytic sheaves (cf. Local cohomology).

Important results concerning extension of analytic subsets are the theorems of Remmert–Stein–Shiffman and Bishop. The Remmert–Stein–Shiffman theorem states that every pure 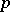-dimensional complex-analytic subset in 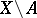, where is a complex-analytic space and 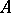a closed subset having zero 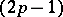-dimensional Hausdorff measure, can be extended to a pure 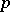-dimensional complex-analytic subset in 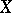. 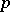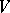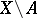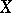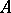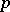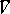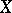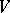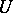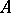Bishop's theorem states that every pure -dimensional complex-analytic subset in , where is a complex-analytic space and is a complex-analytic subset, can be extended to a pure -dimensional complex-analytic subset in if has locally finite volume in some neighbourhood of in .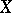

There are criteria for extendability of analytic mappings, generalizing the classical Picard theorem. E.g., every analytic mapping 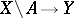, where 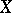is a complex manifold, 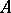is an analytic nowhere-dense set and 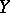is a hyperbolic compact complex manifold, can be extended to an analytic mapping 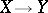. Every analytic mapping 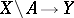that is not everywhere-degenerate, where is a complex manifold, 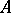is an analytic subset and 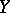is a compact complex manifold with negative first Chern class, can be extended to a meromorphic mapping .

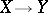References

[1]	P.A. Griffiths, J. King, "Nevanlinna theory and holomorphic mappings between algebraic varieties" Acta. Math. , 130 (1973) pp. 145–220
[2]	S. Kobayashi, "Hyperbolic manifolds and holomorphic mappings" , M. Dekker (1970)
[3]	R. Harvey, "Holomorphic chains and their boundaries" , Proc. Symp. Pure Math. , 30 , Amer. Math. Soc. (1977) pp. 309–382

Comments

Bishop's theorem has been generalized in several directions. Let 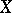be an open subset of 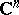and 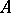a complex-analytic subset of 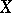. First, Skoda's theorem states that if 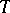is a positive closed current of bi-degree 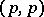on 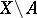which has locally finite mass in a neighbourhood of 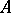, then 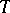extends to a positive closed current on 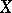. (A current on 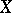is a continuous linear functional on the space of all complex differential forms of class 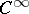on 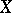, with compact support, in the strong topology, cf. [a1] and Differential form.) Next, H. El Mir showed that one may take 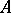to be a closed complete pluripolar set, which is more general than a closed analytic set, and then 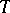as above will still extend. (A pluripolar set 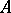in 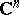is a set such there exists a plurisubharmonic function 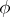defined in some neighbourhood of 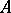such that 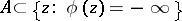, the set of 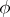. It is a complete pluripolar set if there is such a 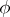with 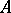equal to the 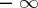set of 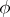.) N. Sibony generalized these results even further: If 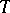is a pluripositive current of bi-degree 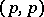on 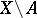which has locally finite mass in a neighbourhood of 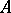, then 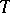extends to a pluripositive current on .

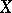One recovers Bishop's theorem from Skoda's using the fact that to every pure 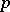-dimensional analytic subset 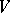of 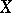is associated a current 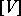, the current of integration over the regular points of 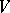. This is a positive closed current of bi-degree 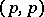. One can return from currents to analytic sets using Siu's theorem (cf. [a4]) on analyticity of sets associated to positive Lelong numbers. (The Lelong number at a point of a pure 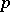-dimensional analytic set 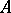in 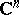is the number

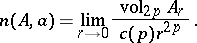The limit exists (cf., e.g., [a1]); in this formula, 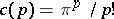, the volume of the unit ball in 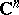, and 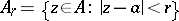(i.e. the part of contained in the ball with centre and radius ), cf. also [a1].)

References

[a1]	E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian)
[a2]	N. Sibony, "Quelques problèmes de prolongement de courants en analyse complexe" Duke Math. J. , 52 (1985) pp. 157–197
[a3]	Y.T. Siu, "Techniques of extension of analytic objects" , M. Dekker (1974)
[a4]	Y.T. Siu, "Analyticity of sets associated to Lelong numbers and the extension of closed positive currents" Inv. Math. , 27 (1974) pp. 53–156