Extension of a semi-group
A semi-group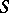 
containing the given semi-group 
as a sub-semi-group. One is usually concerned with extensions that are in some way related to the given semi-group 
. The most well-developed theory is that of ideal extensions (those semi-groups containing 
as an ideal). To each element 
of an ideal extension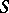 
of a semi-group 
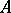are assigned its left and right translations 
, 
: 
, 
(
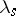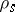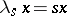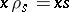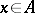); let 
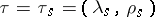. The mapping 
is a homomorphism of 
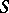into the translation hull 
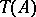of 
, and is an isomorphism in the case when 
is weakly reductive (see Translations of semi-groups). The semi-group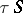 
is called the type of the ideal extension 
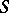. Among the ideal extensions 
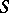of 
, one can distinguish strong extensions, for which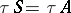 
, and pure extensions, for which 
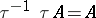. Every ideal extension of 
is a pure extension of one of its strong extensions.
An ideal extension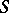 
of 
is called dense (or essential) if every homomorphism of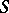 
that is injective on 
is an isomorphism. 
has a maximal dense ideal extension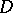 
if and only if 
is weakly reductive. In this case,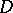 
is unique up to an isomorphism and is isomorphic to 
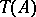. Also, in this case, 
is called a densely-imbedded ideal in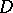 
. The sub-semi-groups of 
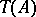containing 
, and only these, are isomorphic to dense ideal extensions of a weakly reductive semi-group 
.
If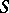 
is an ideal extension of 
and if the quotient semi-group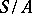 
is isomorphic to 
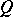, then 
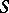is called an extension of 
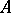by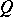 
. The following cases have been studied extensively: ideal extensions of completely-simple semi-groups, of a group by a completely 
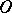-simple semi-group, of a commutative semi-group with cancellation by a group with added zero, etc. In general, the problem of describing all ideal extensions of a semi-group 
by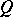 
is far from being solved.
Among other types of extensions of 
one can mention semi-groups that have a congruence with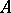 
as one of its classes, and in particular the so-called Schreier extensions of a semi-group with identity [1], which are analogues of Schreier extensions of groups. In studying the various forms of extensions of a semi-group (in particular, for inverse semi-groups), one uses cohomology of semi-groups.
Another broad area in the theory of extensions of semi-groups is concerned with various problems on the existence of extensions of a semi-group 
that belong to a given class. Thus, any semi-group 
can be imbedded in a complete semi-group, in a simple semi-group (relative to congruences), or in a bi-simple semi-group with zero and an identity (see Simple semi-group), and any finite or countable semi-group can be imbedded in a semi-group with two generators. Conditions are known under which a semi-group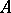 
can be imbedded in a semi-group without proper left ideals, in an inverse semi-group (cf. Inversion semi-group), in a group (see Imbedding of semi-groups), etc.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1 , Amer. Math. Soc. (1961) |
| [2] | M. Petrich, "Introduction to semigroups" , C.E. Merrill (1973) |
Extension of a semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extension_of_a_semi-group&oldid=46881