Exponential mapping
A mapping of the tangent space of a manifold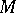 
into 
. It is defined by a connection given on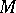 
and is a far-reaching generalization of the ordinary exponential function regarded as a mapping of a straight line into itself.
1) Let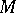 
be a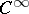 
-manifold with an affine connection, let 
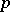be a point in 
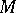, let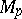 
be the tangent space to 
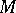at 
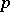, let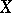 
be a non-zero vector in 
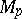, and let 
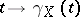be the geodesic passing through 
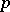in the direction of 
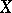. There is an open neighbourhood 
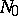of the point 
in 
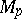and an open neighbourhood 
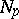of 
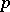in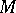 
such that the mapping 
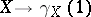is a diffeomorphism of 
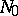onto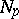 
. This mapping is called the exponential mapping at 
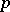and is denoted by 
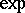. A neighbourhood 
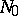is called normal if: 1) the mapping 
maps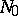 
onto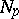 
diffeomorphically; and 2) 
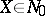and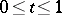 
imply that 
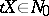. In this case 
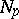is said to be a normal neighbourhood of the point 
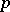in the manifold 
. Every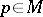 
has a convex normal neighbourhood 
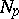: Any two points of such a neighbourhood can be joined by exactly one geodesic segment lying in 
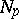. If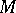 
is a complete Riemannian manifold, then 
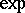is a surjective mapping of 
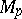onto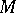 
.
2) Let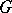 
be a Lie group with identity 
and let 
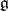be the corresponding Lie algebra consisting of the tangent vectors to 
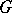at 
. For every vector 
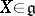there is a unique differentiable homomorphism 
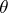of the group 
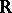into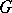 
such that the tangent vector to 
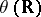at 
coincides with 
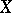. The mapping 
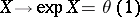is called the exponential mapping of the algebra 
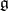into the group 
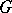. There is an open neighbourhood 
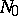of the point 
in 
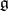and an open neighbourhood 
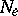of 
in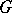 
such that 
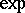is a diffeomorphism of 
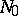onto 
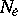. Let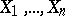 
be some basis for the algebra 
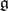. The mapping 
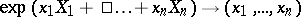is a coordinate system on 
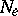; these coordinates are called canonical.
The concept of an exponential mapping of a Lie group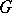 
can also be approached from another point of view. There is a one-to-one correspondence between the set of all affine connections on 
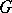that are invariant relative to the group of left translations and the set of bilinear functions 
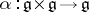. It turns out that the exponential mapping 
of the algebra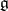 
into the group 
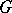coincides with the mapping 
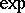of the tangent space of 
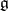into the manifold 
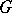at the point 
in this manifold with respect to the left-invariant affine connection corresponding to any skew-symmetric bilinear function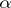 
.
References
| [1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Exponential mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exponential_mapping&oldid=46876