Euclidean connection

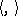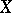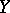A differential-geometric structure on a Euclidean vector bundle, generalizing the Levi-Civita connection, or Riemannian connection, in Riemannian geometry. A smooth vector bundle is called Euclidean if each of its fibres has the structure of a Euclidean vector space with a scalar product such that for any smooth sections and the function is a smooth function on the base. A linear connection on a Euclidean vector bundle is called a Euclidean connection if for any parallel displacement of two vectors their scalar product remains constant. This is equivalent to the metric tensor defining the scalar product 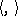in each fibre being covariantly constant. The Euclidean connection in the tangent bundle of a Riemannian space is the Riemannian connection. Sometimes the term "Euclidean connection" is used only in this case, and then "Riemannian connection" means the Levi-Civita connection.

Comments

The Euclidean connection is also sometimes called the metric connection.

References

[a1]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963)
[a2]	W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) pp. Chapt. 1.8 (Translated from German)