Equivalent representations

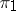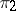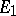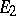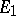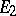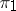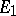Two representations and of a group (algebra, ring, semi-group) in vector spaces and , respectively, for which there is an intertwining operator which is a vector space isomorphism from to (sometimes such representations are called algebraically equivalent); if and are representations in topological vector spaces and 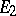, then 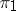and 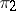are called topologically equivalent if there is an intertwining operator for 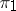and 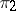which is a topological vector space isomorphism from 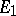to 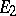. The term "equivalent representations" is also used to define some other equivalence relations: For example, two representations are called weakly equivalent if there is a closed operator with a dense domain of definition and a dense range that intertwines these representations. Two representations of a Lie group in Banach spaces are called infinitesimally equivalent if the induced representations of the universal enveloping algebra on their spaces of analytic vectors are algebraically equivalent. Two representations of an algebra are sometimes called equivalent, or isomorphic, if their kernels coincide; two representations of a topological group are called equivalent if the induced representations of some group algebra of this group are isomorphic.