Equivalence of dynamical systems
Two autonomous systems of ordinary differential equations (cf. Autonomous system)
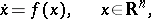 | (a1) |
and
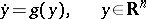 | (a2) |
(and their associated flows, cf. Flow (continuous-time dynamical system)), are topologically equivalent [a1], [a2], [a3] if there exists a homeomorphism 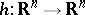 ,
, 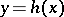 , which maps orbits of (a1) into orbits of (a2) preserving the direction of time. The systems (a1) and (a2) are locally topologically equivalent near the origin if
, which maps orbits of (a1) into orbits of (a2) preserving the direction of time. The systems (a1) and (a2) are locally topologically equivalent near the origin if 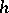 is defined in a small neighbourhood of
is defined in a small neighbourhood of 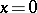 and
and  .
.
If the systems depend on parameters, the definition of topological equivalence is modified as follows. Two families of ordinary differential equations,
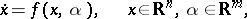 | (a3) |
and
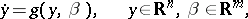 | (a4) |
are called topologically equivalent if:
i) there is a homeomorphism 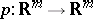 ,
, 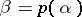 ;
;
ii) there is a family of parameter-dependent homeomorphisms 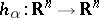 ,
, 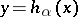 , mapping orbits of (a3) at parameter values
, mapping orbits of (a3) at parameter values 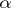 into orbits of (a4) at parameter values
into orbits of (a4) at parameter values 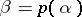 .
.
The systems (a3) and (a4) are locally topologically equivalent near the origin, if the mapping 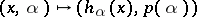 is defined in a small neighbourhood of
is defined in a small neighbourhood of 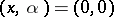 in
in 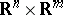 and
and 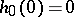 ,
, 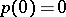 .
.
The above definitions are applicable verbatim to discrete-time dynamical systems defined by iterations of diffeomorphisms.
References
| [a1] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Grundlehren math. Wiss. , 250 , Springer (1983) (In Russian) |
| [a2] | J. Guckenheimer, Ph. Holmes, "Nonlinear oscillations, dynamical systems and bifurcations of vector fields" , Springer (1983) |
| [a3] | Yu.A. Kuznetsov, "Elements of applied bifurcation theory" , Springer (1995) |
Equivalence of dynamical systems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equivalence_of_dynamical_systems&oldid=46842