Enumerated model
A pair  , where
, where  is a model of a certain fixed signature
is a model of a certain fixed signature 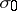 and
and  is an enumeration of the underlying set
is an enumeration of the underlying set 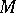 of
of 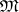 . The most extensively developed trend in the study of enumerated models is recursive model theory. Another is the investigation of the problem of the complexity of an enumerated model, by which one means the complexity of the set of natural numbers
. The most extensively developed trend in the study of enumerated models is recursive model theory. Another is the investigation of the problem of the complexity of an enumerated model, by which one means the complexity of the set of natural numbers 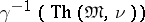 , or of the set
, or of the set 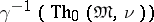 , where
, where  is a certain Gödel enumeration of all formulas of the signature
is a certain Gödel enumeration of all formulas of the signature 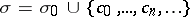 . Here the constants
. Here the constants  do not belong to
do not belong to  ,
,  is the set of all closed formulas of
is the set of all closed formulas of 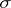 that are true in the system
that are true in the system 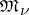 which is obtained from
which is obtained from 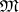 by enriching
by enriching  to
to  , the value of the constant
, the value of the constant  being put equal to
being put equal to  , and
, and 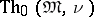 denotes the set of all quantifier-free formulas that are true in
denotes the set of all quantifier-free formulas that are true in  .
.
Various special models of elementary theories (cf. Elementary theory) play an important role in mathematical logic and algebra. One of the important problems is that of their complexity. The following results have been obtained. Let 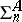 ,
, 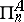 ,
,  and
and 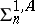 ,
, 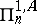 ,
,  denote, respectively, the arithmetic and analytic hierarchies relative to
denote, respectively, the arithmetic and analytic hierarchies relative to  (cf. Hierarchy).
(cf. Hierarchy).
If a theory  is recursive relative to
is recursive relative to  and has a simple model
and has a simple model  , then there exists an enumeration
, then there exists an enumeration  of
of 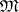 such that
such that  , that is
, that is  is recursive with respect to the set
is recursive with respect to the set  of all Gödel numbers
of all Gödel numbers  of those computable functions
of those computable functions 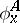 relative to
relative to 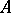 for which
for which 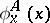 is defined.
is defined.
If  is recursive relative to
is recursive relative to 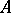 and has a countable saturated model
and has a countable saturated model  , then there exists an enumeration
, then there exists an enumeration  of
of 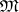 such that
such that  , that is,
, that is,  is a hyper-arithmetic set relative to
is a hyper-arithmetic set relative to  ; these bounds on the complexity are in a certain sense exact.
; these bounds on the complexity are in a certain sense exact.
The following result is also connected with the task of finding exact bounds. It is known that every non-contradictory formula has an enumerated model  of complexity
of complexity  , that is
, that is
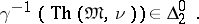 |
The Ershov hierarchy gives a finer classification of the sets in  . The following theorem has been proved: For any
. The following theorem has been proved: For any  there exists a non-contradictory formula
there exists a non-contradictory formula 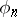 that has no enumerated model
that has no enumerated model 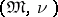 with predicates in
with predicates in 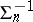 , that is,
, that is, 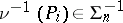 and
and 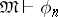 , where
, where  . In a constructive non-atomic Boolean algebra
. In a constructive non-atomic Boolean algebra 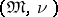 one can construct a recursively-enumerable ideal
one can construct a recursively-enumerable ideal  (that is, the set
(that is, the set 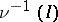 is recursively enumerable) such that the Boolean algebra
is recursively enumerable) such that the Boolean algebra  is not constructive. This makes it possible to prove that the lattice of recursively-enumerable sets is not recursively presentable.
is not constructive. This makes it possible to prove that the lattice of recursively-enumerable sets is not recursively presentable.
The study of enumerated total orders has made it possible to disprove the conjecture of the strong homogeneity of the Turing degrees.
References
| [1] | S.S. Goncharov, B.N. Drobotun, "Numerations of saturated and homogeneous models" Siberian Math. J. , 21 (1980) pp. 183–190 Sibirsk. Mat. Zh. , 21 : 2 (1980) pp. 25–41 |
| [2] | S.D. Denisov, "Models of a non-contradictory formula and the hierarchy of Eshov" Algebra and Logic , 11 (1972) pp. 359–362 Algebra i Logika , 11 : 6 (1972) pp. 648–655 |
| [3] | B.N. Drobotun, "Enumerations of simple models" Siberian Math. J. , 18 (1977) pp. 707–716 (In Russian) Sibirsk. Mat. Zh. , 18 : 5 (1977) pp. 1002–1014 |
| [4] | Yu.L. Ershov, "Theorie der Numierungen" , I-II , Deutsch. Verlag Wissenschaft. (1973–1976) (Translated from Russian) |
| [5] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165 |
| [6] | L. Feiner, "Hierarchies of Boolean algebras" J. Symbolic Logic , 35 (1970) pp. 365–374 |
| [7] | L. Feiner, "The strong homogeneity conjecture" J. Symbolic Logic , 35 (1970) pp. 375–377 |
Enumerated model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Enumerated_model&oldid=46829