Energy integral
A quantity representing the sum of the kinetic and the potential energy of a mechanical system at a certain moment in time.
Suppose, for example, that in a bounded domain 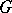 with piecewise-smooth boundary
with piecewise-smooth boundary 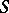 for a hyperbolic partial differential equation
for a hyperbolic partial differential equation
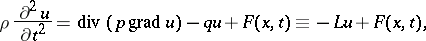 | (1) |
where
 |
one poses the mixed problem
 | (2) |
 | (3) |
 |
A classical solution of (2)–(3) is a function  of class
of class 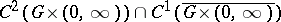 satisfying (1) in the cylinder
satisfying (1) in the cylinder 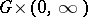 , the initial conditions (2) on the lower base, and the boundary condition (3) on the lateral surface of the cylinder.
, the initial conditions (2) on the lower base, and the boundary condition (3) on the lateral surface of the cylinder.
Then the relation
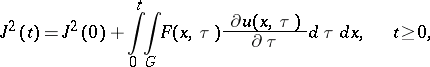 | (4) |
holds, where
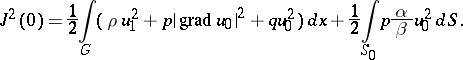 |
The energy integral is defined as the quantity
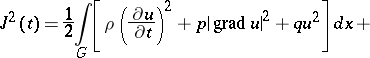 |
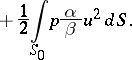 |
For 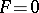 equality (4) takes the form
equality (4) takes the form
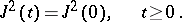 |
The physical meaning of the energy integral consists in the fact that the total energy of an oscillating system in the absence of external perturbations does not change in time (the law of conservation of energy).
References
| [1] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) MR0764399 Zbl 0954.35001 Zbl 0652.35002 Zbl 0695.35001 Zbl 0699.35005 Zbl 0607.35001 Zbl 0506.35001 Zbl 0223.35002 Zbl 0231.35002 Zbl 0207.09101 |
Comments
References
| [a1] | O.A. Ladyzhenskaya, N.N. Ural'tseva, "Equations aux dérivées partielles de type elliptique" , Dunod (1969) (Translated from Russian) Zbl 0164.13001 |
| [a2] | O.A. Ladyzhenskaya, V.A. Solonnikov, N.N. Ural'tseva, "Linear and quasi-linear equations of parabolic type" , Amer. Math. Soc. (1968) (Translated from Russian) Zbl 0174.15403 |
| [a3] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1966) MR0208121 Zbl 0143.32403 |
| [a4] | F. John, "Partial differential equations" , Springer (1978) MR0514404 MR0502136 MR0470380 Zbl 0456.65060 Zbl 0426.35002 Zbl 0413.93002 Zbl 0397.35041 Zbl 0396.35037 Zbl 0381.35059 Zbl 0377.65045 Zbl 0368.34003 |
| [a5] | P.R. Garabedian, "Partial differential equations" , Wiley (1967) MR1657375 MR0943117 MR0162045 MR0176086 MR0129167 MR0120441 MR0060698 MR0054819 MR0046440 Zbl 0913.35001 Zbl 0124.30501 Zbl 0133.04402 Zbl 0096.06503 Zbl 0058.08902 Zbl 0050.10002 |
Energy integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Energy_integral&oldid=46822