Emden equation
The non-linear second-order ordinary differential equation
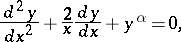 | (1) |
or, in self-adjoint form,
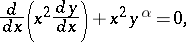 |
where 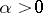 ,
,  , is a constant. The point
, is a constant. The point 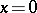 is singular for the Emden equation. By the change of variable
is singular for the Emden equation. By the change of variable  equation (1) becomes
equation (1) becomes
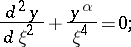 |
and by the change of variable 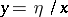 ,
,
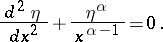 |
After the changes of variables
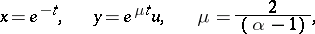 |
and subsequent lowering of the order by the substitution  , one obtains the first-order equation
, one obtains the first-order equation
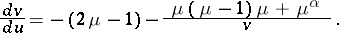 |
Equation (1) was obtained by R. Emden [1] in connection with a study of equilibrium conditions for a polytropic gas ball; this study led him to the problem of the existence of a solution of (1) with the initial conditions 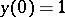 ,
, 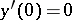 , defined on a certain segment
, defined on a certain segment 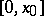 ,
, 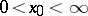 , and having the properties
, and having the properties
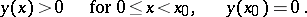 |
Occasionally (1) is also called the Lienard–Emden equation.
More general than Emden's equation is the Fowler equation
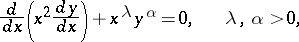 |
and the Emden–Fowler equation
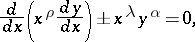 | (2) |
where 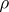 ,
, 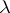 ,
,  are real parameters. As a special case this includes the Thomas–Fermi equation
are real parameters. As a special case this includes the Thomas–Fermi equation
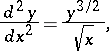 |
which arises in the study of the distribution of electrons in an atom. If 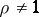 , then by a change of variables (2) can be brought to the form
, then by a change of variables (2) can be brought to the form
 |
There are various results in the qualitative and asymptotic investigation of solutions of the Emden–Fowler equation (see, for example, [2], [3]). A detailed study has also been made of the equation of Emden–Fowler type
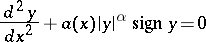 |
(on this and its analogue of order  see [4]).
see [4]).
References
| [1] | R. Emden, "Gaskugeln" , Teubner (1907) |
| [2] | G. Sansone, "Equazioni differenziali nel campo reale" , 2 , Zanichelli (1949) |
| [3] | R.E. Bellman, "Stability theory of differential equations" , McGraw-Hill (1953) |
| [4] | I.T. Kiguradze, "Some singular boundary value problems for ordinary differential equations" , Tbilisi (1975) (In Russian) |
Emden equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Emden_equation&oldid=46818