Ellipse of normal curvature
A geometrical construction characterizing the distribution of the curvatures at a certain point on a regular surface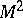 
in the 
-dimensional Euclidean space 
. Let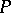 
be a point on a surface 
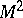and let 
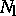be the 
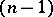-dimensional subspace containing the normal space 
to 
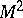at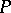 
and the tangent to 
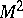at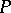 
in the direction 
. The section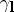 
of 
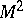by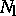 
is called a normal section at 
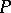. The vector 
, lying in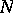 
, where 
is the natural parameter on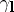 
, is called the vector of normal curvature of 
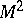in the direction 
. The end points of the vectors of normal curvature form the ellipse of normal curvature.
For a two-dimensional surface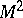 
with non-zero Gaussian curvature in 
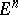to lie in a certain three-dimensional subspace 
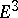it is necessary and sufficient that its ellipse of normal curvature at all points 
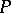degenerates to a segment passing through 
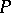(see ).
Similarly one defines the indicatrix of curvature for a submanifold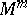 
of arbitrary dimension 
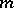. It is an 
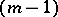-dimensional algebraic surface of order 
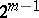. The vectors of normal curvature form a cone which, together with the tangent space to 
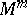, determines a subspace 
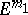, the so-called domain of curvature of 
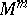at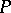 
. The dimension 
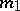of this subspace satisfies
 |
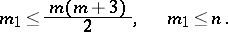Points at which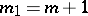 
are called axial, those at which 
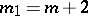— planar, and those at which 
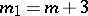— spatial. Sometimes one considers for submanifolds of large codimension the Dupin indicatrix, the construction of which is completely analogous to that of the Dupin indicatrix for a surface in three-dimensional space.
References
| [1] | J.A. Schouten, D.J. Struik, "Einführung in die neueren Methoden der Differentialgeometrie" , 2 , Noordhoff (1935) |
| [2a] | Yu.A. Aminov, "Torsion of two-dimensional surfaces in Euclidean spaces" Ukrain. Geom. Sb. , 17 (1975) pp. 3–14 (In Russian) |
| [2b] | Yu.A. Aminov, "An analogue of Ricci's condition for a minimal variety in a Riemannian space" Ukrain. Geom. Sb. , 17 (1975) pp. 15–22; 144 (In Russian) |
Comments
References
| [a1] | M. do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) |
| [a2] | B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) |
| [a3] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1969) pp. Chapt. 7 |
| [a4] | M. Spivak, "A comprehensive introduction to differential geometry" , 3 , Publish or Perish pp. 1–5 |
Ellipse of normal curvature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ellipse_of_normal_curvature&oldid=46805