Elementary events

An initial concept in a probability model. In the definition of a probability space 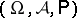the non-empty set is called the space of elementary events and any point 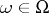is an elementary event. In an informal approach, describes the set of all outcomes of a certain random experiment and an elementary event 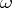corresponds to an elementary outcome: the experiment ends with one and only one elementary outcome, these outcomes are indecomposable and mutually exclusive. 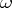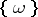There is a fundamental difference between an elementary event , a point of , and the event , an element of a certain class of sets 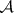. See Probability theory; Probability space; Random event.