Dyad

A linear transformation on a Hilbert space

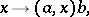where and 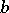are certain constant vectors and 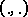is the inner product. The importance of a dyad is due to the fact that, for example, in an -dimensional space any linear transformation can be represented as the sum of at most dyads:

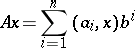(in an arbitrary Hilbert space a similar decomposition is valid for special classes of linear operators, for example self-adjoint operators, where 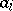and can be chosen to form a biorthogonal system). Attempts were made in the 19th century to base the theory of linear operators on the concept of a dyad — the so-called "dyadic calculus" — but the term dyad is used only rarely in our own days.

References

[1]	Ya.S. Dubnov, "Fundamentals of vector calculus" , 1–2 , Moscow-Leningrad (1950–1952) (In Russian)
[2]	M. Lagally, "Vorlesungen über Vektor-rechnung" , Becker & Erler (1944)
[3]	S. Chapman, T.G. Cowling, "The mathematical theory of non-uniform gases" , Cambridge Univ. Press (1939)

References

[a1]	M.R. Spiegel, "Vector analysis and an introduction to tensor analysis" , McGraw-Hill (1959)