Drift equations
Approximate equations of motion of a charged particle in electric and magnetic fields, obtained by averaging the rapid motion of the particle under the effect of the magnetic field. Drift equations apply if the magnetic field 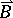 is changing slowly in space and in time, while the electric field
is changing slowly in space and in time, while the electric field 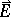 is small as compared to the magnetic field:
is small as compared to the magnetic field:
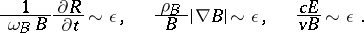 | (1) |
Here  is a small parameter,
is a small parameter, 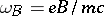 is the Larmor frequency,
is the Larmor frequency,  is the Larmor radius,
is the Larmor radius,  is the velocity of the particle, and
is the velocity of the particle, and 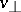 is the velocity component in the direction normal to the magnetic field. Drift equations are obtained from the complete equations of motion by expanding in powers of
is the velocity component in the direction normal to the magnetic field. Drift equations are obtained from the complete equations of motion by expanding in powers of  with the aid of the averaging method [1]. They have the following form:
with the aid of the averaging method [1]. They have the following form:
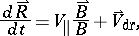 | (2) |
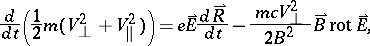 | (3) |
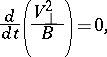 | (4) |
where
 |
The system (2)–(4), known as the drift system, is written with respect to the auxiliary averaged variables 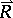 ,
, 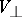 ,
, 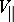 , connected by a certain relation with the initial variables
, connected by a certain relation with the initial variables 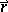 ,
, 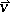 . The drift rate
. The drift rate 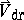 in equation (2) describes a slow motion along the averaged trajectory in the direction perpendicular to the magnetic field:
in equation (2) describes a slow motion along the averaged trajectory in the direction perpendicular to the magnetic field:
 |
The equations (3) and (4) have second-order accuracy with respect to  and define the magnitudes
and define the magnitudes 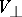 and
and 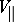 up to first order terms in the time interval
up to first order terms in the time interval 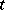 containing many Larmor periods
containing many Larmor periods 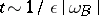 . Equation (2) has first-order accuracy with respect to
. Equation (2) has first-order accuracy with respect to  .
.
The magnitude  , which is the integral of the drift system (2)–(4), is an approximate integral of the true motion. It is known as the adiabatic invariant. In the static case, when
, which is the integral of the drift system (2)–(4), is an approximate integral of the true motion. It is known as the adiabatic invariant. In the static case, when  and
and 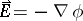 , equation (3) admits the energy integral
, equation (3) admits the energy integral
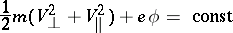 |
for the averaged motion.
The drift system may be generalized to include the relativistic case [2], [3].
References
| [1] | N.N. Bogolyubov, Yu.A. Mitropol'skii, "Asymptotic methods in the theory of non-linear oscillations" , Hindushtan Publ. Comp. , Delhi (1961) (Translated from Russian) |
| [2] | D.V. Sivukhin, , Problems in the theory of plasma , 1 , Moscow (1963) pp. 7–97 (In Russian) |
| [3] | A.I. Morozov, L.S. Solov'ev, , Problems in the theory of plasma , 2 , Moscow (1963) pp. 177–261 (In Russian) |
Drift equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Drift_equations&oldid=46776