Double-layer potential
An expression of the type
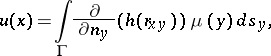 | (1) |
where 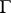 is the boundary of an arbitrary bounded
is the boundary of an arbitrary bounded 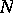 -dimensional domain
-dimensional domain 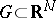 ,
, 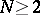 , and
, and 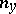 is the exterior normal to the boundary
is the exterior normal to the boundary 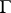 of
of  at a point
at a point 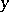 ;
; 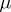 is the potential density, which is a function defined on
is the potential density, which is a function defined on 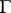 ;
; 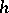 is a fundamental solution of the Laplace equation:
is a fundamental solution of the Laplace equation:
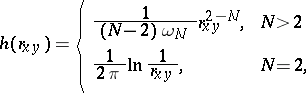 | (2) |
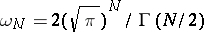 is the area of the surface of the
is the area of the surface of the 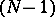 -dimensional unit sphere, and
-dimensional unit sphere, and 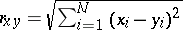 is the distance between two points
is the distance between two points  and
and 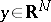 . The boundary
. The boundary 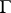 is of class
is of class 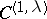 ; it is a Lyapunov surface or a Lyapunov arc (cf. Lyapunov surfaces and curves).
; it is a Lyapunov surface or a Lyapunov arc (cf. Lyapunov surfaces and curves).
Expression (1) may be interpreted as the potential produced by dipoles located on 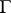 , the direction of which at any point
, the direction of which at any point 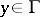 coincides with that of the exterior normal
coincides with that of the exterior normal  , while its intensity is equal to
, while its intensity is equal to 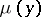 .
.
If 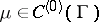 , then
, then  is defined on
is defined on 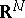 (in particular, on
(in particular, on 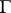 ) and displays the following properties.
) and displays the following properties.
1) The function  has derivatives of all orders
has derivatives of all orders 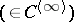 everywhere in
everywhere in  and satisfies the Laplace equation, and the derivatives with respect to the coordinates of a point may be computed by differentiation of the integrand.
and satisfies the Laplace equation, and the derivatives with respect to the coordinates of a point may be computed by differentiation of the integrand.
2) On passing through the boundary 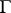 the function
the function  undergoes a break. Let
undergoes a break. Let 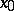 be an arbitrary point on
be an arbitrary point on 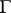 ; let
; let 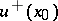 and
and 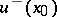 be the interior and exterior boundary values; then
be the interior and exterior boundary values; then 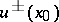 exist and are equal to
exist and are equal to
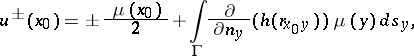 | (3) |
and the integral in formula (3) as a function of 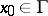 belongs to
belongs to 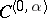 for any
for any 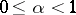 ; also, the function equal to
; also, the function equal to  in
in 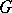 and to
and to 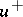 on
on  is continuous on
is continuous on 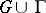 , while the function equal to
, while the function equal to  in
in 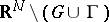 and equal to
and equal to 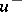 on
on 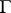 is continuous in
is continuous in 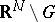 .
.
3) If the density 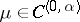 and if
and if 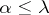 , then
, then  , extended as in (2) on
, extended as in (2) on 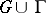 or
or 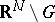 , is of class
, is of class 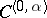 in
in 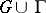 or in
or in 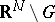 .
.
4) If 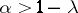 , and
, and 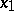 and
and 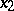 are two points on the normal issuing from a point
are two points on the normal issuing from a point 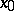 and lying symmetric about
and lying symmetric about 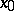 , then
, then
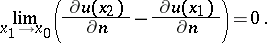 | (4) |
In particular, if one of the derivatives 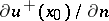 ,
, 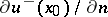 exists, then the other derivative also exists and
exists, then the other derivative also exists and 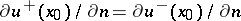 . This is also true if
. This is also true if 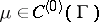 and
and 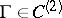 .
.
The above properties can be generalized in various ways. The density 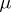 may belong to
may belong to 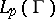 ,
,  . Then
. Then 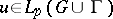 ,
, 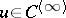 outside
outside 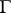 and it satisfies the Laplace equation, formula (3) and (4) apply for almost-all
and it satisfies the Laplace equation, formula (3) and (4) apply for almost-all 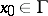 and the integral in (3) belongs to
and the integral in (3) belongs to 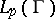 .
.
The properties of double-layer potentials, regarded as integrals with respect to an arbitrary measure  defined on
defined on 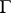 , have also been studied:
, have also been studied:
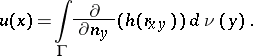 |
Here, too, 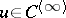 outside
outside 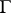 and it satisfies the Laplace equation. Formulas (3) and (4) apply for almost-all
and it satisfies the Laplace equation. Formulas (3) and (4) apply for almost-all 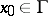 with respect to the Lebesgue measure
with respect to the Lebesgue measure  after
after 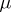 has been replaced by the density
has been replaced by the density 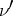 . In definition (1) the fundamental solution of the Laplace equation may be replaced by an arbitrary Lewy function for a general elliptic operator of the second order with variable coefficients, while
. In definition (1) the fundamental solution of the Laplace equation may be replaced by an arbitrary Lewy function for a general elliptic operator of the second order with variable coefficients, while 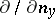 is replaced by the derivative with respect to the conormal. The properties listed above remain valid [2].
is replaced by the derivative with respect to the conormal. The properties listed above remain valid [2].
The double-layer potential plays an important role in solving boundary value problems of elliptic equations. The representation of the solution of the (first) boundary value problem is sought as a double-layer potential with unknown density 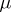 and an application of property (2) leads to a Fredholm equation of the second kind on
and an application of property (2) leads to a Fredholm equation of the second kind on 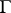 in order to determine the function
in order to determine the function 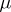 [1], [2]. In solving boundary value problems for parabolic equations use is made of the concept of the thermal double layer potential, i.e. of an integral of the type
[1], [2]. In solving boundary value problems for parabolic equations use is made of the concept of the thermal double layer potential, i.e. of an integral of the type
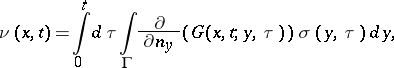 |
where 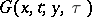 is a fundamental solution of the thermal conductance (or heat) equation in an
is a fundamental solution of the thermal conductance (or heat) equation in an 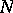 -dimensional space:
-dimensional space:
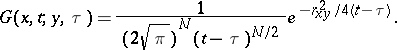 |
Here, 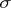 is the potential density. The function
is the potential density. The function  and its generalization to the case of an arbitrary parabolic equation of the second order have properties which are similar to those described above for
and its generalization to the case of an arbitrary parabolic equation of the second order have properties which are similar to those described above for  [3], [4], [5].
[3], [4], [5].
References
| [1] | N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from French) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [3] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [4] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [5] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
Comments
See [a1] for an introduction to double-layer potentials for more general open sets in 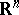 .
.
References
| [a1] | J. Král, "Integral operators in potential theory" , Lect. notes in math. , 823 , Springer (1980) |
Double-layer potential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Double-layer_potential&oldid=46766